Triton Kernels - Fused Softmax

Fused Softmax Triton kernel exploration

Posted Sep 18, 2025 Updated Sep 24, 2025

By Kapil Sharma

18 min read

Softmax is one of the most fundamental operations in modern neural networks, particularly in attention mechanisms and classification layers. It’s especially critical in transformer architectures where it’s used extensively in self-attention computations. Unlike simple element-wise operations, softmax requires row-wise reductions (like RMSNorm), making it an excellent candidate for efficient Triton kernel implementation.

What is Softmax?

Softmax converts a vector of real numbers into a probability distribution. Each output element is in the range (0,1) and all elements sum to 1. The mathematical formula is:

\[\text{softmax}(x_i) = \frac{e^{x_i}}{\sum_{j=1}^{n} e^{x_j}}\]

Where:

$x_i$ is the $i$-th input element
$n$ is the number of elements in the input vector
The output is a probability distribution over $n$ classes

Numerical Stability in Softmax

A naive implementation of softmax can suffer from numerical overflow when dealing with large input values. The numerically stable version subtracts the maximum value from each element:

\[\text{softmax}(x_i) = \frac{e^{x_i - \max(x)}}{\sum_{j=1}^{n} e^{x_j - \max(x)}}\]

This ensures that the largest exponent is 0, preventing overflow while maintaining mathematical equivalence.

Softmax Triton Kernel

Softmax shares similarities with RMSNorm in that it requires row-wise reductions followed by point-wise operations. The key differences are:

Two reduction passes: Finding max, then computing sum of exponentials
Exponential operations: More computationally expensive than squares
Probability constraint: Output must sum to exactly 1.0

Let’s walk through a concrete example showing how softmax works in a Triton kernel with block-level processing:

Example Setup

Consider a 3×8 input matrix where each row needs independent softmax normalization with BLOCK_SIZE=4:

Input Matrix:
Row 0: [ 2.0, -1.0,  3.0,  0.5, -0.5,  1.5, -2.0,  1.0]
Row 1: [ 4.0, -3.0,  2.5,  1.0, -1.5,  0.0, -0.5,  2.0]
Row 2: [-1.0,  3.5, -2.5,  1.5,  0.0, -3.0,  2.5, -0.5]

Step 1: Program ID Mapping

Each Triton program (CUDA block) processes one row independently:

  
row_id = tl.program_id(0)  # Each CUDA block processes one row

# Base pointers for this row
in_row_ptr = input_ptr + row_id * n_cols
out_row_ptr = output_ptr + row_id * n_cols

Block Assignment:

Program 0: Processes Row 0
Program 1: Processes Row 1
Program 2: Processes Row 2

Step 2: Find Maximum Value (First Reduction)

With BLOCK_SIZE=4, each row is processed in 2 blocks to find the maximum:

Row 0 Processing (Program ID 0):

  
# Triton kernel code for finding max
row_max = -float('inf')
for start in range(0, n_cols, BLOCK_SIZE):  # start = 0, then start = 4
    cols = start + tl.arange(0, BLOCK_SIZE)  # [0,1,2,3] then [4,5,6,7]
    mask = cols < n_cols
    vals = tl.load(in_row_ptr + cols, mask=mask, other=-float('inf'))
    row_max = tl.maximum(row_max, tl.max(vals, axis=0))

Block	Columns	Values	Block Max	Global Max
Block 1	0-3	`[2.0, -1.0, 3.0, 0.5]`	3.0	3.0
Block 2	4-7	`[-0.5, 1.5, -2.0, 1.0]`	1.5	3.0

All Rows Maximum Summary:

Row	Values	Maximum
Row 0	`[2.0, -1.0, 3.0, 0.5, -0.5, 1.5, -2.0, 1.0]`	3.0
Row 1	`[4.0, -3.0, 2.5, 1.0, -1.5, 0.0, -0.5, 2.0]`	4.0
Row 2	`[-1.0, 3.5, -2.5, 1.5, 0.0, -3.0, 2.5, -0.5]`	3.5

Step 3: Compute Sum of Exponentials (Second Reduction)

Now we compute $\sum e^{x_i - \max(x)}$ for numerical stability:

  
# Use the row_max found in previous step
row_sum = 0.0
for start in range(0, n_cols, BLOCK_SIZE):
    cols = start + tl.arange(0, BLOCK_SIZE)
    mask = cols < n_cols
    vals = tl.load(in_row_ptr + cols, mask=mask, other=0.0)
    row_sum += tl.sum(tl.exp(vals - row_max), axis=0)

Row 0 Exponential Sum (max = 3.0):

Block	Original Values	Stable Values (x-max)	Exponentials	Block Sum
Block 1	`[2.0, -1.0, 3.0, 0.5]`	`[-1.0, -4.0, 0.0, -2.5]`	`[0.368, 0.018, 1.000, 0.082]`	1.468
Block 2	`[-0.5, 1.5, -2.0, 1.0]`	`[-3.5, -1.5, -5.0, -2.0]`	`[0.030, 0.223, 0.007, 0.135]`	0.395
			Total Sum	1.863

All Rows Exponential Sum Summary:

Row	Maximum	Sum of Exponentials
Row 0	3.0	1.863
Row 1	4.0	3.717
Row 2	3.5	4.982

Step 4: Compute Softmax Output

Finally, we compute the softmax: $\frac{e^{x_i - \max(x)}}{\sum e^{x_j - \max(x)}}$

  
# Use the row_sum computed in previous step
for start in range(0, n_cols, BLOCK_SIZE):
    cols = start + tl.arange(0, BLOCK_SIZE)
    mask = cols < n_cols
    vals = tl.load(in_row_ptr + cols, mask=mask, other=0.0)
    out = tl.exp(vals - row_max) / row_sum  # Compute softmax
    tl.store(out_row_ptr + cols, out, mask=mask)

Row 0 Softmax Computation (row_max=3.0, row_sum=1.863):

Block	Original Values	Stable Values (vals-row_max)	Exponentials	Softmax Output
Block 1	`[2.0, -1.0, 3.0, 0.5]`	`[-1.0, -4.0, 0.0, -2.5]`	`[0.368, 0.018, 1.000, 0.082]`	`[0.197, 0.010, 0.537, 0.044]`
Block 2	`[-0.5, 1.5, -2.0, 1.0]`	`[-3.5, -1.5, -5.0, -2.0]`	`[0.030, 0.223, 0.007, 0.135]`	`[0.016, 0.120, 0.004, 0.072]`

Complete Output Matrix

After processing all rows:

Output Matrix (Softmax Applied):
Row 0: [0.197, 0.010, 0.537, 0.044, 0.016, 0.120, 0.004, 0.072]  # Sum = 1.000
Row 1: [0.546, 0.001, 0.184, 0.041, 0.003, 0.015, 0.009, 0.110]  # Sum = 1.000
Row 2: [0.012, 0.665, 0.003, 0.083, 0.030, 0.001, 0.203, 0.018]  # Sum = 1.000

Softmax Kernel

The optimized softmax implementation uses a hybrid approach that automatically selects the best strategy based on the input size:

Two-Path Strategy

Fast Path: When the entire row fits within BLOCK_SIZE - single-pass computation
Tiled Path: When rows are larger than BLOCK_SIZE - multi-pass block processing

This approach maximizes performance across different tensor sizes and hardware configurations.

  
import triton
import triton.language as tl

@triton.jit
def softmax_forward(
    input_ptr,             # pointer to [n_rows, n_cols]
    output_ptr,            # pointer to [n_rows, n_cols]
    n_rows: tl.constexpr,  # number of rows
    n_cols: tl.constexpr,  # number of columns (feature dim)
    BLOCK_SIZE: tl.constexpr
):
    row_id = tl.program_id(0)

    # Base pointers for this row
    in_row_ptr = input_ptr + row_id * n_cols
    out_row_ptr = output_ptr + row_id * n_cols

    # ---- Fast path: entire row fits in BLOCK_SIZE ----
    if n_cols <= BLOCK_SIZE:
        col_offsets = tl.arange(0, BLOCK_SIZE)
        mask = col_offsets < n_cols
        vals = tl.load(in_row_ptr + col_offsets, mask=mask, other=-float('inf')).to(tl.float32)

        row_max = tl.max(vals, axis=0)
        vals_stable = vals - row_max
        numer = tl.exp(vals_stable)
        denom = tl.sum(numer, axis=0)
        out = numer / denom

        tl.store(out_row_ptr + col_offsets, out, mask=mask)
        return

    # ---- Tiled path: handle rows larger than BLOCK_SIZE ----
    # ==== Reduction Pass ====
    # Pass 1: compute row max
    row_max = -float('inf')
    for start in range(0, n_cols, BLOCK_SIZE):
        cols = start + tl.arange(0, BLOCK_SIZE)
        mask = cols < n_cols
        vals = tl.load(in_row_ptr + cols, mask=mask, other=-float('inf')).to(tl.float32)
        row_max = tl.maximum(row_max, tl.max(vals, axis=0))

    # ==== Reduction Pass ====
    # Pass 2: compute exp-sum
    row_sum = 0.0
    for start in range(0, n_cols, BLOCK_SIZE):
        cols = start + tl.arange(0, BLOCK_SIZE)
        mask = cols < n_cols
        vals = tl.load(in_row_ptr + cols, mask=mask, other=0.0).to(tl.float32)
        row_sum += tl.sum(tl.exp(vals - row_max), axis=0)

    # ==== Pointwise pass ====
    # Pass 3: normalize + write
    for start in range(0, n_cols, BLOCK_SIZE):
        cols = start + tl.arange(0, BLOCK_SIZE)
        mask = cols < n_cols
        vals = tl.load(in_row_ptr + cols, mask=mask, other=0.0).to(tl.float32)
        out = tl.exp(vals - row_max) / row_sum
        tl.store(out_row_ptr + cols, out, mask=mask)

Fast Path (Small Rows)

For small feature dimensions (n_cols <= BLOCK_SIZE), we can load the entire row into registers and compute everything in a single pass:

  
# Fast path: entire row fits in BLOCK_SIZE
if n_cols <= BLOCK_SIZE:
    col_offsets = tl.arange(0, BLOCK_SIZE)
    mask = col_offsets < n_cols
    vals = tl.load(in_row_ptr + col_offsets, mask=mask, other=-float('inf'))

    row_max = tl.max(vals, axis=0)          # Find maximum
    vals_stable = vals - row_max            # Numerical stability
    numer = tl.exp(vals_stable)             # Compute exponentials
    denom = tl.sum(numer, axis=0)           # Sum for normalization
    out = numer / denom                     # Final softmax

    tl.store(out_row_ptr + col_offsets, out, mask=mask)
    return

Benefits of Fast Path:

Single memory load: Data loaded once and kept in registers
No redundant computation: All operations happen on cached data
Optimal for small sequences: Common in many attention patterns

Tiled Path (Large Rows)

UPDATE (2025-09-24): On performance debugging, I later realized that the tiled path is never executed because I was always passing BLOCK_SIZE = max(triton.next_power_of_2(n_cols), 64). FWIW, when I capped the BLOCK_SIZE, the kernel performance wasn’t great as soon we hit vocab dimension of >=1024. It seems to suggest that the block size strategy in the kernel is fine. Below, we still cover the tiled approach for demostration purposes.

For larger feature dimensions, we use the three-pass approach with block processing:

Pass 1: Find Row Maximum

  
row_max = -float('inf')
for start in range(0, n_cols, BLOCK_SIZE):
    cols = start + tl.arange(0, BLOCK_SIZE)
    mask = cols < n_cols
    vals = tl.load(in_row_ptr + cols, mask=mask, other=-float('inf'))
    row_max = tl.maximum(row_max, tl.max(vals, axis=0))

Pass 2: Compute Sum of Exponentials

  
row_sum = 0.0
for start in range(0, n_cols, BLOCK_SIZE):
    cols = start + tl.arange(0, BLOCK_SIZE)
    mask = cols < n_cols
    vals = tl.load(in_row_ptr + cols, mask=mask, other=0.0)
    row_sum += tl.sum(tl.exp(vals - row_max), axis=0)

Pass 3: Normalize and Store

  
for start in range(0, n_cols, BLOCK_SIZE):
    cols = start + tl.arange(0, BLOCK_SIZE)
    mask = cols < n_cols
    vals = tl.load(in_row_ptr + cols, mask=mask, other=0.0)
    out = tl.exp(vals - row_max) / row_sum
    tl.store(out_row_ptr + cols, out, mask=mask)

Benefits of Tiled Path:

Memory efficiency: Handles arbitrarily large sequences
Numerical stability: Consistent max subtraction across all blocks
Parallelizable: Each block can be processed independently within each pass

Let’s see it in action

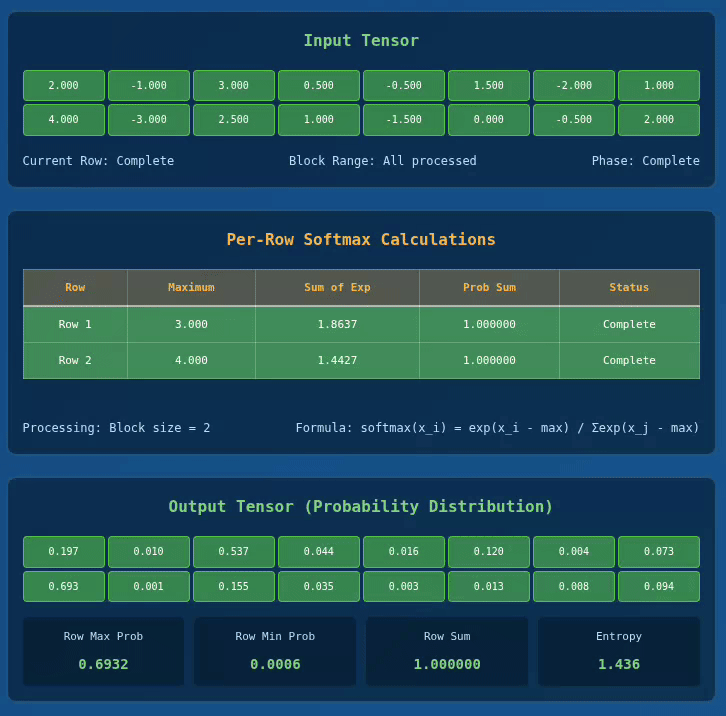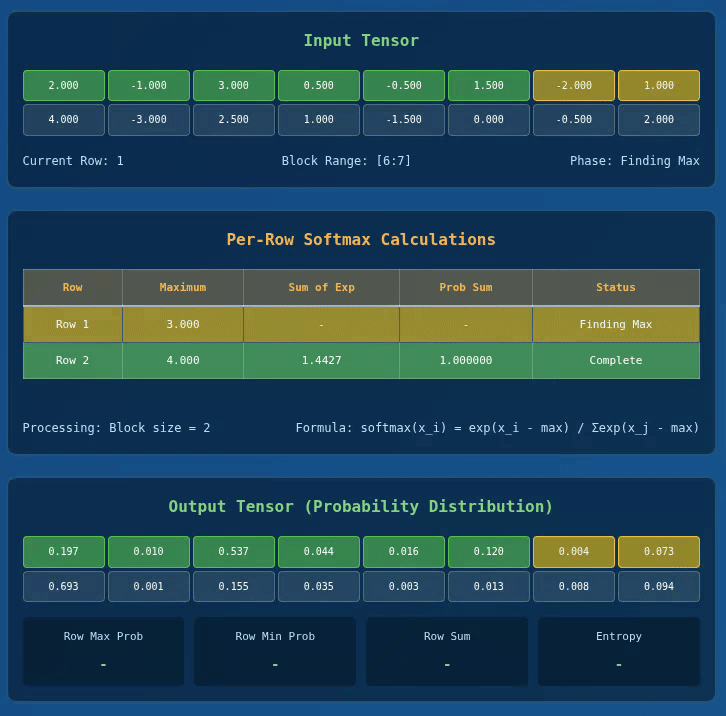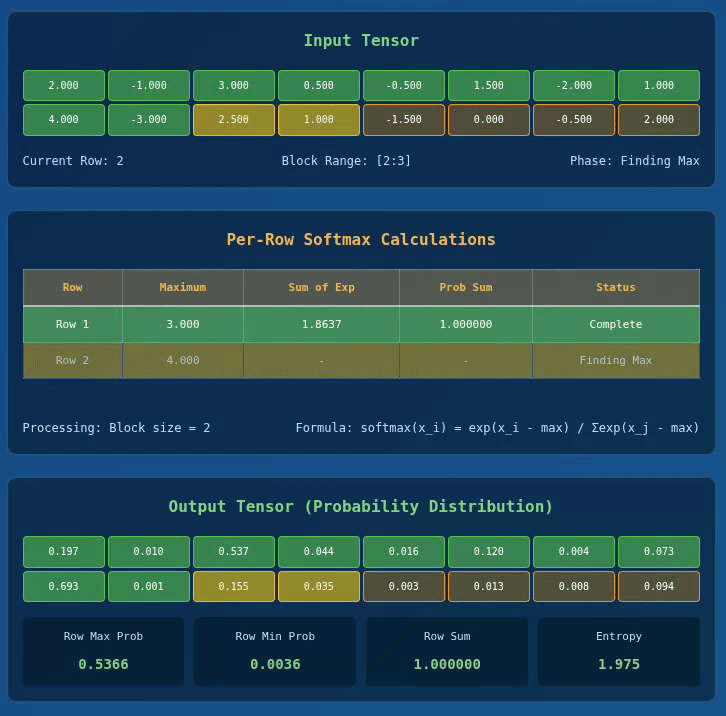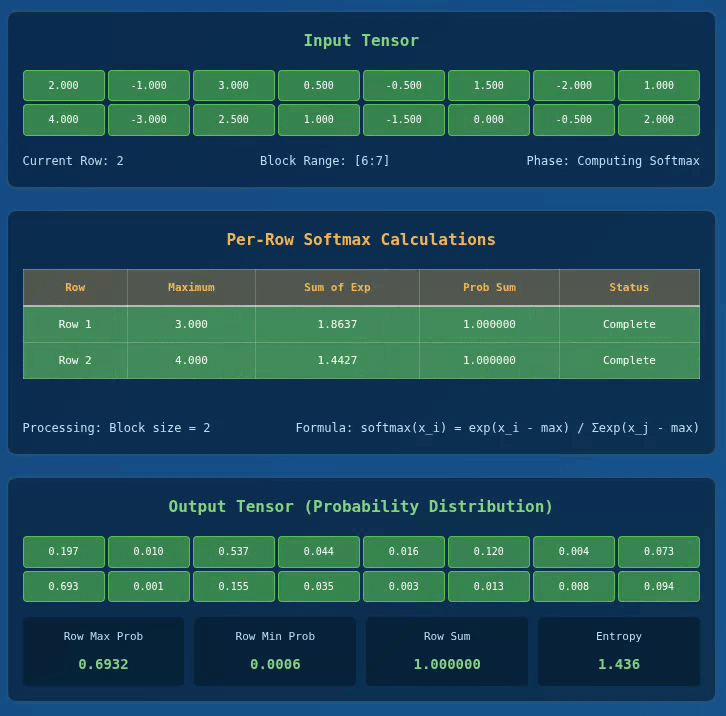
Below we have a visualization for 2 x 8 Tensor with BLOCK_SIZE = 2:

Interactive Softmax Visualizer

Explore how Softmax activation works in Triton kernels with this interactive visualization:

🎯 Softmax Activation Triton Kernel Visualization

Rows (Batch Size)

Feature Dimension

Block Size

Input Tensor

Current Row: - Block Range: - Phase: -

Per-Row Softmax Calculations

Row	Maximum	Sum of Exp	Prob Sum	Status

Processing: Block size = 4 Formula: softmax(x_i) = exp(x_i - max) / Σexp(x_j - max)

Output Tensor (Probability Distribution)

Row Max Prob

Row Min Prob

Row Sum

Entropy

Optimization and Numeric Strategies

Memory Access Patterns

Softmax kernels benefit from several optimization strategies:

Coalesced Memory Access: Ensure consecutive threads access consecutive memory locations
Shared Memory Usage: Store intermediate results in shared memory for reuse
Register Blocking: Minimize memory traffic by keeping frequently accessed data in registers

Numerical Precision

  
# High-precision accumulation for better numerical stability
_sum = tl.zeros([BLOCK_SIZE], dtype=tl.float64)  # Use double precision for sum
# ... accumulate in double precision ...
sum_exp = tl.sum(_sum, axis=0).to(tl.float32)   # Convert back for final computation

Fusion Opportunities

Softmax is often fused with other operations:

  
# Fused Softmax + Cross-Entropy Loss
@triton.jit
def softmax_cross_entropy_fused(
    logits_ptr, targets_ptr, loss_ptr,
    row_stride, feature_dim, BLOCK_SIZE: tl.constexpr
):
    # Compute softmax and cross-entropy in a single kernel
    # Saves memory bandwidth by avoiding intermediate softmax storage
    pass

# Fused Attention Softmax
@triton.jit
def attention_softmax_fused(
    query_ptr, key_ptr, value_ptr, output_ptr,
    seq_len, head_dim, BLOCK_SIZE: tl.constexpr
):
    # Compute Q@K^T, apply softmax, then multiply by V
    # Reduces memory traffic in attention computation
    pass

Typical Use Cases

Softmax is critical in several key areas:

1. Attention Mechanisms

  
# Scaled Dot-Product Attention
attention_scores = Q @ K.T / sqrt(d_k)
attention_weights = softmax(attention_scores)  # Softmax over sequence dimension
output = attention_weights @ V

2. Classification Layers

  
# Multi-class classification
logits = model(input)
probabilities = softmax(logits)  # Convert to probability distribution
predicted_class = argmax(probabilities)

3. Language Model Sampling

  
# Temperature-scaled softmax for text generation
scaled_logits = logits / temperature
probabilities = softmax(scaled_logits)
next_token = sample(probabilities)

Benchmarks

Let’s see triton benchmarks with our softmax kernel implementation compared to PyTorch:

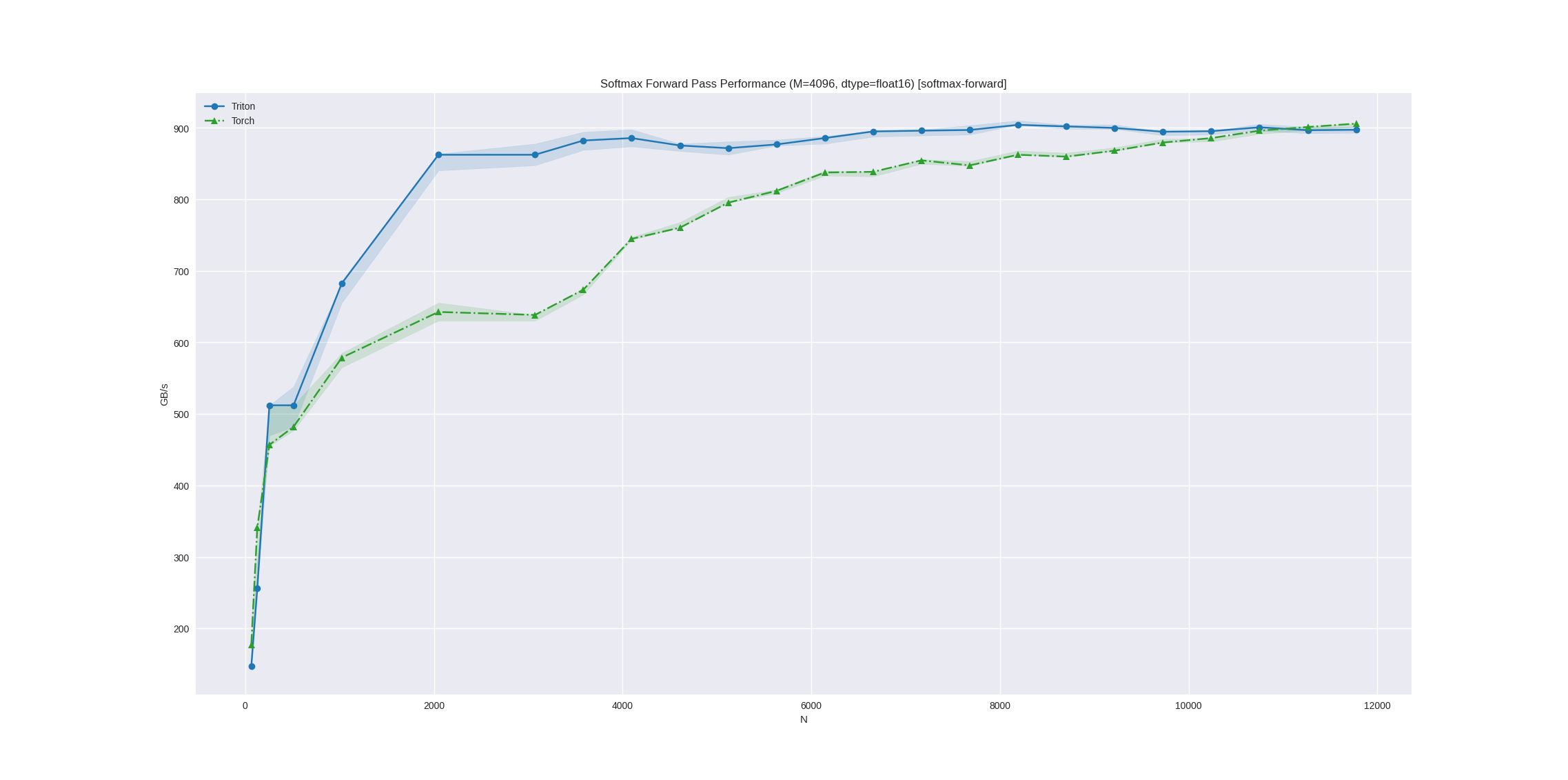
The benchmark shows our Triton implementation achieving competitive performance with PyTorch’s optimized kernels for small batches.

Looking at this benchmark data, we can see that for larger vocabulary sizes (N > ~1024), Triton performance plateaus around 870-900 GB/s while PyTorch continues to scale, reaching similar performance levels at the highest vocabulary sizes.

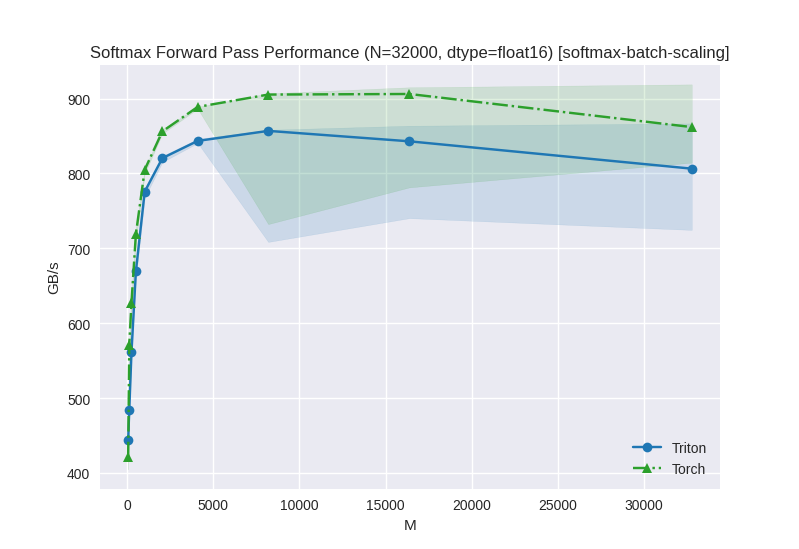
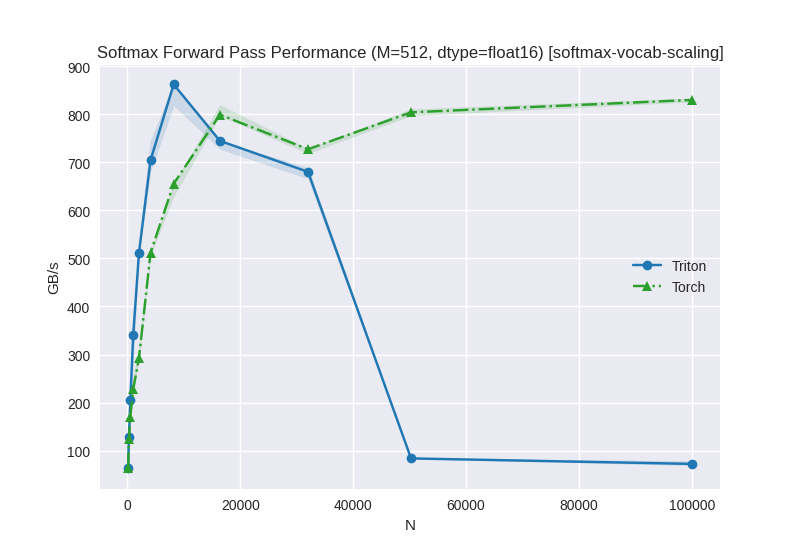
For vocabulary scaling, Triton outperforms PyTorch at medium sizes (512-8192) but shows significant performance degradation at very large vocabularies (32K+), while PyTorch maintains consistent throughput across all vocabulary sizes.

Perf Debugging

I created a sample script to now look at each implementation separately to see what are the bottlenecks in the triton kernel for batch size and vocab scaling.

  
#!/usr/bin/env python3

import sys
import torch
import click
from loguru import logger

# Import the existing softmax kernel
from kernels.softmax import softmax

# Ensure CUDA is available
if not torch.cuda.is_available():
    logger.error("CUDA is not available. This script requires a CUDA-capable GPU.")
    sys.exit(1)

DEVICE = torch.device("cuda")


def benchmark_softmax(
    M, N, dtype=torch.float16, warmup_iters=10, bench_iters=100, backend="triton"
):
    """
    Benchmark softmax kernel with specific M and N values.

    Args:
        M: Number of rows (batch dimension)
        N: Number of columns (feature dimension)
        dtype: Data type for tensors
        warmup_iters: Number of warmup iterations
        bench_iters: Number of benchmark iterations
        backend: Either "triton" or "torch"
    """
    logger.info(f"Benchmarking {backend} softmax with M={M}, N={N}, dtype={dtype}")

    # Create input tensor
    x = torch.randn(M, N, dtype=dtype, device=DEVICE) * 2.0

    # Select softmax function
    if backend == "triton":
        softmax_fn = softmax
    elif backend == "torch":
        softmax_fn = lambda x: torch.nn.functional.softmax(x, dim=-1)
    else:
        raise ValueError(f"Unknown backend: {backend}")

    # Warmup
    logger.info(f"Warming up for {warmup_iters} iterations...")
    for _ in range(warmup_iters):
        _ = softmax_fn(x)
    torch.cuda.synchronize()

    # Benchmark
    logger.info(f"Running benchmark for {bench_iters} iterations...")

    # Collect individual timings for noise reduction
    times_ms = []

    for _ in range(bench_iters):
        torch.cuda.synchronize()
        start_event = torch.cuda.Event(enable_timing=True)
        end_event = torch.cuda.Event(enable_timing=True)

        start_event.record()
        output = softmax_fn(x)
        end_event.record()

        torch.cuda.synchronize()
        times_ms.append(start_event.elapsed_time(end_event))

    # Remove top and bottom 10% to reduce noise
    times_ms.sort()
    n_remove = int(0.1 * len(times_ms))
    if n_remove > 0:
        trimmed_times = times_ms[n_remove:-n_remove]
        logger.info(f"Trimmed {n_remove} outliers from each end ({2*n_remove} total)")
    else:
        trimmed_times = times_ms

    avg_time_ms = sum(trimmed_times) / len(trimmed_times)

    # Calculate metrics
    num_elements = M * N
    bytes_accessed = 2 * num_elements * x.element_size()  # input + output
    bandwidth_gbps = (bytes_accessed * 1e-9) / (avg_time_ms * 1e-3)

    logger.success(f"Benchmark completed:")
    logger.info(f"  Average time per iteration: {avg_time_ms:.4f} ms")
    logger.info(f"  Bandwidth: {bandwidth_gbps:.2f} GB/s")
    logger.info(f"  Total elements: {num_elements:,}")
    logger.info(f"  Memory accessed: {bytes_accessed / 1e9:.2f} GB")

    return output, avg_time_ms, bandwidth_gbps


@click.command()
@click.option("--M", type=int, required=True, help="Number of rows (batch dimension)")
@click.option(
    "--N", type=int, required=True, help="Number of columns (feature dimension)"
)
@click.option(
    "--backend",
    type=click.Choice(["triton", "torch"]),
    default="triton",
    help="Backend to use: triton (custom kernel) or torch (PyTorch)",
)
@click.option(
    "--dtype",
    type=click.Choice(["float16", "float32"]),
    default="float16",
    help="Data type for tensors",
)
@click.option("--warmup", type=int, default=10, help="Number of warmup iterations")
@click.option("--iters", type=int, default=100, help="Number of benchmark iterations")
@click.option(
    "--profile-only", is_flag=True, help="Run only a single iteration for profiling"
)
def main(m, n, backend, dtype, warmup, iters, profile_only):
    """Benchmark softmax kernel for ncu profiling."""

    # Convert dtype string to torch dtype
    dtype_map = {"float16": torch.float16, "float32": torch.float32}
    dtype_tensor = dtype_map[dtype]

    logger.info(f"Starting {backend} softmax benchmark with parameters:")
    logger.info(f"  Backend: {backend}")
    logger.info(f"  M (rows): {m}")
    logger.info(f"  N (cols): {n}")
    logger.info(f"  dtype: {dtype}")
    logger.info(f"  warmup iterations: {warmup}")
    logger.info(f"  benchmark iterations: {iters}")

    if profile_only:
        logger.info("Profile-only mode: running single iteration for ncu profiling")
        x = torch.randn(m, n, dtype=dtype_tensor, device=DEVICE) * 2.0

        if backend == "triton":
            output = softmax(x)
        else:  # torch
            output = torch.nn.functional.softmax(x, dim=-1)

        torch.cuda.synchronize()
        logger.success("Single iteration completed for profiling")
    else:
        # Run full benchmark
        output, avg_time_ms, bandwidth_gbps = benchmark_softmax(
            m, n, dtype_tensor, warmup, iters, backend
        )

    logger.success("Benchmark completed successfully!")


if __name__ == "__main__":
    main()

Repro

  
$ python softmax_benchmark.py --M 8192 --N 32000  --iters 1000 --backend torch 
2025-09-19 10:46:09.523 | INFO     | __main__:main:127 - Starting torch softmax benchmark with parameters:
2025-09-19 10:46:09.523 | INFO     | __main__:main:128 -   Backend: torch
2025-09-19 10:46:09.523 | INFO     | __main__:main:129 -   M (rows): 8192
2025-09-19 10:46:09.523 | INFO     | __main__:main:130 -   N (cols): 32000
2025-09-19 10:46:09.523 | INFO     | __main__:main:131 -   dtype: float16
2025-09-19 10:46:09.523 | INFO     | __main__:main:132 -   warmup iterations: 10
2025-09-19 10:46:09.523 | INFO     | __main__:main:133 -   benchmark iterations: 1000
2025-09-19 10:46:09.524 | INFO     | __main__:benchmark_softmax:36 - Benchmarking torch softmax with M=8192, N=32000, dtype=torch.float16
2025-09-19 10:46:09.588 | INFO     | __main__:benchmark_softmax:50 - Warming up for 10 iterations...
2025-09-19 10:46:09.613 | INFO     | __main__:benchmark_softmax:56 - Running benchmark for 1000 iterations...
2025-09-19 10:46:10.812 | INFO     | __main__:benchmark_softmax:78 - Trimmed 100 outliers from each end (200 total)
2025-09-19 10:46:10.812 | SUCCESS  | __main__:benchmark_softmax:89 - Benchmark completed:
2025-09-19 10:46:10.812 | INFO     | __main__:benchmark_softmax:90 -   Average time per iteration: 1.1638 ms
2025-09-19 10:46:10.812 | INFO     | __main__:benchmark_softmax:91 -   Bandwidth: 901.02 GB/s
2025-09-19 10:46:10.812 | INFO     | __main__:benchmark_softmax:92 -   Total elements: 262,144,000
2025-09-19 10:46:10.812 | INFO     | __main__:benchmark_softmax:93 -   Memory accessed: 1.05 GB
2025-09-19 10:46:10.812 | SUCCESS  | __main__:main:152 - Benchmark completed successfully!

$ python softmax_benchmark.py --M 8192 --N 32000  --iters 1000 --backend triton
2025-09-19 10:46:17.670 | INFO     | __main__:main:127 - Starting triton softmax benchmark with parameters:
2025-09-19 10:46:17.671 | INFO     | __main__:main:128 -   Backend: triton
2025-09-19 10:46:17.671 | INFO     | __main__:main:129 -   M (rows): 8192
2025-09-19 10:46:17.671 | INFO     | __main__:main:130 -   N (cols): 32000
2025-09-19 10:46:17.671 | INFO     | __main__:main:131 -   dtype: float16
2025-09-19 10:46:17.671 | INFO     | __main__:main:132 -   warmup iterations: 10
2025-09-19 10:46:17.671 | INFO     | __main__:main:133 -   benchmark iterations: 1000
2025-09-19 10:46:17.671 | INFO     | __main__:benchmark_softmax:36 - Benchmarking triton softmax with M=8192, N=32000, dtype=torch.float16
2025-09-19 10:46:17.742 | INFO     | __main__:benchmark_softmax:50 - Warming up for 10 iterations...
2025-09-19 10:46:17.932 | INFO     | __main__:benchmark_softmax:56 - Running benchmark for 1000 iterations...
2025-09-19 10:46:19.172 | INFO     | __main__:benchmark_softmax:78 - Trimmed 100 outliers from each end (200 total)
2025-09-19 10:46:19.172 | SUCCESS  | __main__:benchmark_softmax:89 - Benchmark completed:
2025-09-19 10:46:19.172 | INFO     | __main__:benchmark_softmax:90 -   Average time per iteration: 1.2150 ms
2025-09-19 10:46:19.172 | INFO     | __main__:benchmark_softmax:91 -   Bandwidth: 863.02 GB/s
2025-09-19 10:46:19.172 | INFO     | __main__:benchmark_softmax:92 -   Total elements: 262,144,000
2025-09-19 10:46:19.172 | INFO     | __main__:benchmark_softmax:93 -   Memory accessed: 1.05 GB
2025-09-19 10:46:19.172 | SUCCESS  | __main__:main:152 - Benchmark completed successfully!

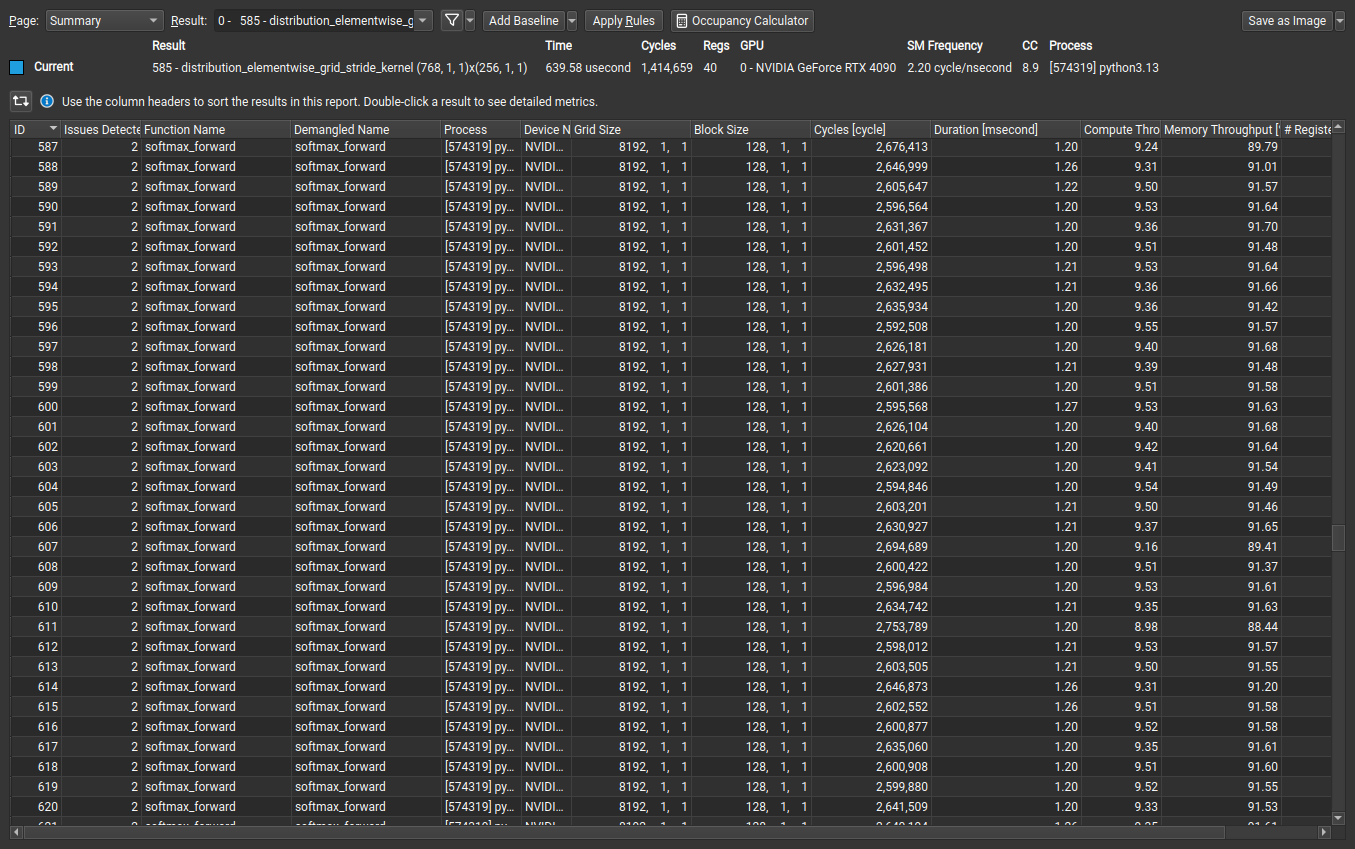
Great! we can repro the difference in memory bandwidth – let’s run the torch and triton versions in ncu.

Triton

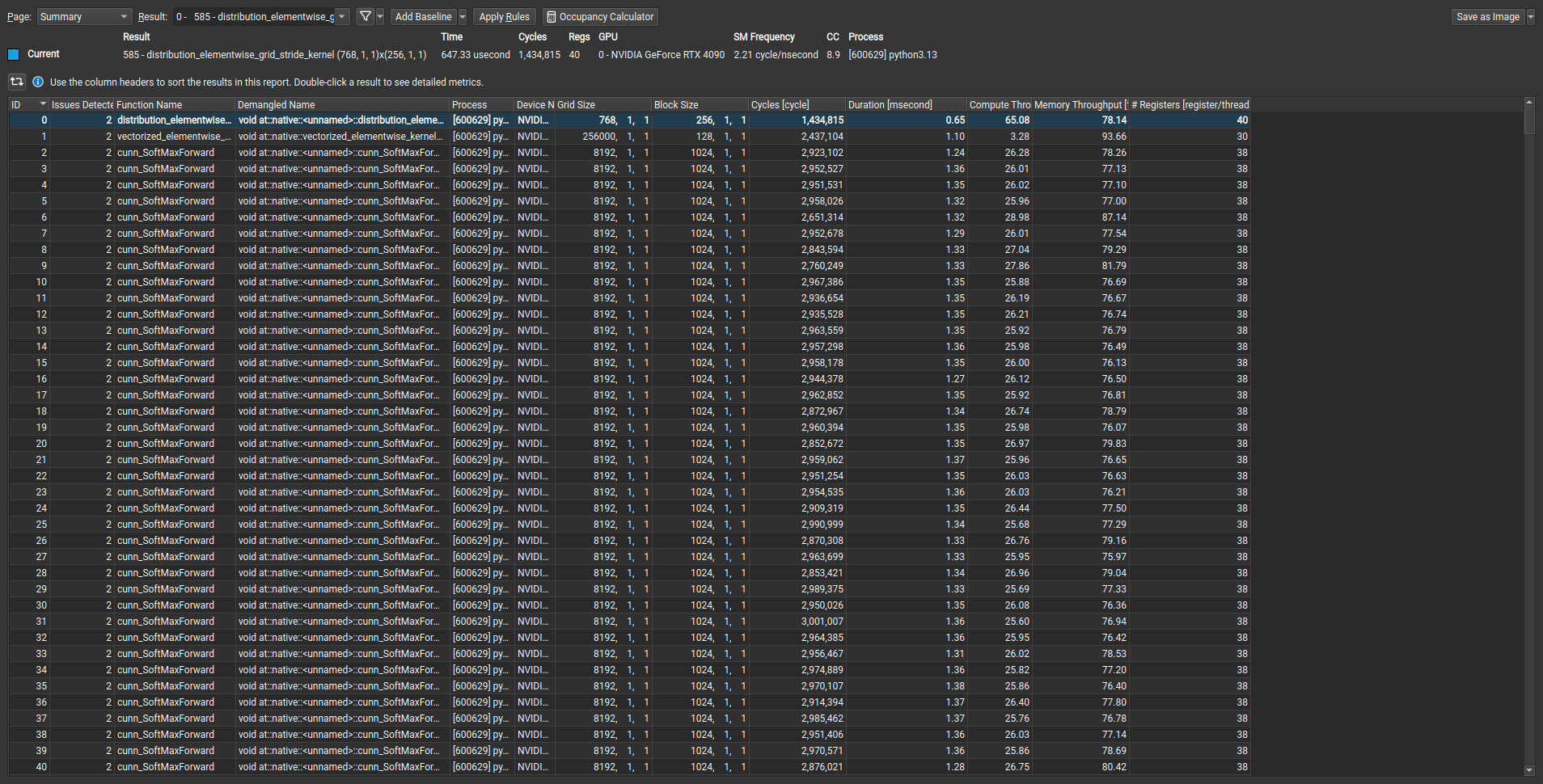
Torch

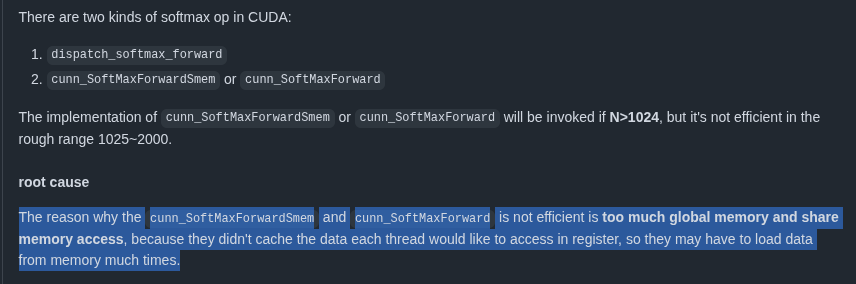
Torch version seems to be calling the cunn_SoftMaxForward kernel under the hood. Seems like there is some discussion on this in a github issue below.

Related GitHub Issue

Softmax kernel performance degradation at large vocabulary sizes #144645

PyTorch performance investigation related to the benchmark results shown above

Update (I missed this originally)

After looking a little closer at the profile, I noticed that the BLOCK_SIZE was automatically changed to 128 in case of the triton kernel versus 1024 for Torch. It seems that triton is autotuning the hard CUDA block size instead of using the logical BLOCK_SIZE that is provided in the kernel.

In addition, when I look at the official tutorial on softmax, they do some shenanigans with the num_warps and warmup.

Summary

In this exploration, I implemented a Triton softmax kernel using a hybrid approach with fast and tiled paths. The kernel achieves competitive performance with PyTorch at small-to-medium vocabulary sizes but shows degradation at very large vocabularies (32K+). Key findings:

Fast path optimization for small sequences (≤ BLOCK_SIZE) enables single-pass computation
Numerical stability maintained through max subtraction across all implementations
Performance trade-offs: Triton excels at medium sizes (512-8192) but PyTorch scales better for large vocabularies

Code

🔗 Triton Kernels Implementation

Blog

This post is licensed under CC BY 4.0 by the author.