Post

Learn CUTLASS the hard way!

Walkthrough of optimization techniques for GEMMs from a naive fp32 kernel to CUTLASS bf16 kernel

Posted Updated
By Kapil Sharma
88 min read
Learn CUTLASS the hard way!

I have been curious about learning the details of GEMMs beyond the basics, i.e., the typical shared memory cache kernel from the PMPP book. There are so many more concepts to learn to understand modern GEMMs, and all of the information is distributed across blog posts, conference talks, etc.

If one is remotely interested in CUDA or Triton programming, they have likely come across this gemm of a post (pun intended) by Simon Boehm, but it was primarily focused on fp32 kernels. The majority of workloads today have shifted to lower precision matmuls such as bf16, fp8, mxfp8, etc. In this post, I’ll walk through several of these optimization stages and go into some detail on tensor cores, WMMA, swizzling, pipelining, autotuning, etc. Pranjal Shankhodhar’s Outperforming cuBLAS on H100 and Aleksa Gordić’s Inside NVIDIA GPUs are two recent posts that I encountered while writing this blog post, and they are really good as well!

My goal was originally to understand a basic CUTLASS kernel. The problem with looking at something like CUTLASS without knowing all the basics is that you will understand the code but not what it is doing under the hood. So, I decided to follow a process to work up to a basic CUTLASS kernel and try to beat PyTorch matmul on my RTX 4090. The whole process and the blog post took me about a month or so and was definitely a rewarding experience!

Prologue

Code

Full implementation of all kernels

In the following sections, we will go over several steps in optimizing GEMM kernel, each time discussing a new concept. Initial sections will look closely into several things Simon covered in his blog post as well. In the later sections, we will look at fp16/bf16 matmul kernels and tensor cores. In the end, we’ll look into CUTLASS kernels and try to optimize/tune it to get the best performance that we can get.

I used Claude Code to create some of the javascript visualizations in this post. I hope readers find them useful. It is not an endorsment of Claude Code but yeah it was pretty good at a lot of javascript tasks. Claude Code was also great at writing some of the python scripts to do plotly graphs for performance benchmarking!

GEMM Basics

GEMM (General Matrix Multiply) is a fundamental operation defined as:

\[C = \alpha AB + \beta C\]

where:

  • $A$ is an $M \times K$ matrix
  • $B$ is a $K \times N$ matrix
  • $C$ is an $M \times N$ matrix (both input and output)
  • $\alpha$ and $\beta$ are scalar coefficients
  • The standard matrix product $C = AB$ is a special case with $\alpha = 1$ and $\beta = 0$
  • When $\beta \neq 0$, GEMM accumulates into a pre-existing matrix $C$
  • This formulation also enables fused operations, avoiding separate kernel launches. We’ll see this in CUTLASS section.

Computational Complexity

Each element $C[i,j]$ requires a dot product:

\[C[i,j] = \alpha \sum_{k=0}^{K-1} A[i,k] \times B[k,j] + \beta C[i,j]\]

For matrices of size $M \times K$, $K \times N$:

  • Total dot products: $M \times N$
  • Operations per dot product: $2K$ (K multiplies + K adds) + 3 scalar ops for linear transformation with $\alpha$, $\beta$
  • Total FLOPs: $2MNK + MK$ (dominated by dot products)

For a $4096 \times 4096$ matrix multiplication ($M = N = K = 4096$):

  • Total operations: $2 \times 4096^3 \approx 137$ GFLOPs
  • Memory required: $3 \times 4096^2 \times 4$ bytes $\approx$ 201 MB (float32)

Hardware Specifications

All benchmarks in this post were run on NVIDIA GeForce RTX 4090. Below are the key specifications:

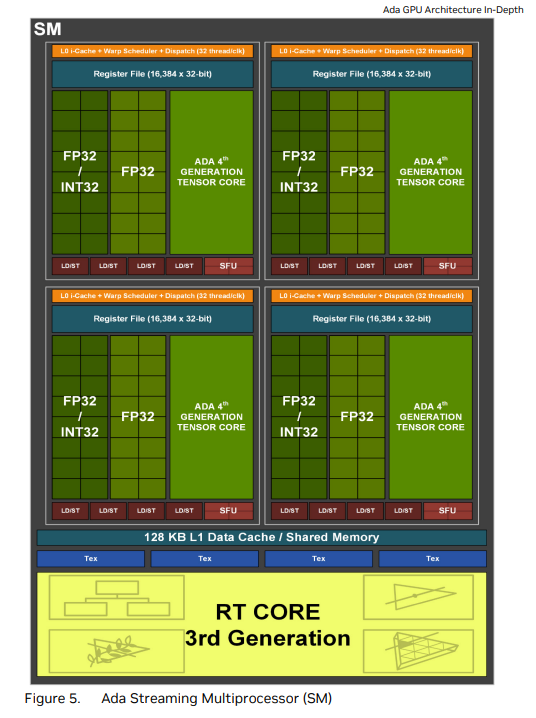
SM Architecture

SM architecture

SpecificationRTX 4090 (Ada Lovelace)
ArchitectureAda Lovelace
CUDA Cores16,384
Streaming Multiprocessors (SMs)128
FP32 Performance82.6 TFLOPS
Tensor Cores512 (4th Gen)
Tensor Performance (FP8)660.6 TFLOPS
RT Cores128 (3rd Gen)
Memory Size24 GB GDDR6X
Memory Bandwidth1,008 GB/s
L1 Cache / Shared Memory (Total)16,384 KB (16 MB)
L2 Cache72 MB
Shared Memory per SM128 KB
Registers per SM256 KB

Source: NVIDIA Ada GPU Architecture Whitepaper

You can load these details directly using cudaDeviceProp as well:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

std::cout << "Number of CUDA devices: " << deviceCount << "\n\n";

for (int i = 0; i < deviceCount; ++i) {
    cudaDeviceProp prop;
    cudaGetDeviceProperties(&prop, i);

    std::cout << "Device " << i << ": " << prop.name << "\n";
    std::cout << "  Compute capability: " << prop.major << "." << prop.minor << "\n";
    std::cout << "  Total global memory: " << (prop.totalGlobalMem >> 20) << " MB\n";
    std::cout << "  Shared memory per block: " << prop.sharedMemPerBlock << " bytes\n";
    std::cout << "  Shared memory per SM: " << prop.sharedMemPerMultiprocessor << " bytes\n";
    std::cout << "  Registers per block: " << prop.regsPerBlock << "\n";
    std::cout << "  Warp size: " << prop.warpSize << "\n";
    std::cout << "  Max threads per block: " << prop.maxThreadsPerBlock << "\n";
    std::cout << "  Max threads per SM: " << prop.maxThreadsPerMultiProcessor << "\n";
    std::cout << "  Number of SMs: " << prop.multiProcessorCount << "\n";
    std::cout << "  Max blocks per SM: " << prop.maxBlocksPerMultiProcessor << "\n";
    std::cout << "  Max grid dimensions: ["
                << prop.maxGridSize[0] << ", "
                << prop.maxGridSize[1] << ", "
                << prop.maxGridSize[2] << "]\n";
    std::cout << "  Max threads dim (block): ["
                << prop.maxThreadsDim[0] << ", "
                << prop.maxThreadsDim[1] << ", "
                << prop.maxThreadsDim[2] << "]\n";
    std::cout << "  Clock rate: " << prop.clockRate / 1000 << " MHz\n";
    std::cout << "  Memory Clock Rate: " << prop.memoryClockRate / 1000 << " MHz\n";
    std::cout << "  Memory Bus Width: " << prop.memoryBusWidth << " bits\n";
    std::cout << "  L2 Cache Size: " << prop.l2CacheSize << " bytes\n";
    std::cout << "  Registers per SM: " << prop.regsPerMultiprocessor << " registers\n";
    std::cout << "  Registers per Block: " << prop.regsPerBlock;
    std::cout << "  Registers per Block: " << prop.warpSize;

    std::cout << std::endl;
}

Roofline Model

Roofline model helps us visualize the performance limitations of our GEMM kernels. I use the numbers for RTX 4090 below:

  1. Compute Bound (flat ceiling): Maximum FLOPS achievable (82.6 TFLOPS for FP32)
  2. Memory Bound (diagonal line): Performance limited by memory bandwidth (1,008 GB/s)

The transition point between memory-bound and compute-bound occurs at an arithmetic intensity of approximately 82 FLOP/byte. Modern optimized GEMM operations typically have high arithmetic intensity, making them compute-bound workloads.

Let’s look at some kernels now…

Naive Implementation

Concept

The simplest approach to calculate GEMM assigns each thread to compute one output element.

What does the memory access pattern look like in this naive case?

At a high level, each thread independently:

  1. Loads one row of $A$ (K elements)
  2. Loads one column of $B$ (K elements)
  3. Computes dot product
  4. Writes one element to $C$

Kernel

Here is a naive implementation for matrix multiply GEMM kernel:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

template <const uint block_size>
__global__ void sgemm_naive_kernel(int num_rows_a, int num_cols_b, int num_cols_a,
                                   float alpha, const float *matrix_a,
                                   const float *matrix_b, float beta, float *output_matrix)
{
    // Map 1D thread ID to 2D output position
    const int output_row = blockIdx.x * block_size + (threadIdx.x % block_size);
    const int output_col = blockIdx.y * block_size + (threadIdx.x / block_size);

    // Boundary check for non-multiple of block size
    if (output_row < num_rows_a && output_col < num_cols_b)
    {
        float accumulator = 0.0f;
        for (int k_idx = 0; k_idx < num_cols_a; ++k_idx)
        {
            accumulator += matrix_a[output_row * num_cols_a + k_idx] *
                           matrix_b[k_idx * num_cols_b + output_col];
        }
        // C = α*(A@B)+β*C
        const int output_idx = output_row * num_cols_b + output_col;
        output_matrix[output_idx] = alpha * accumulator + beta * output_matrix[output_idx];
    }
}

Caller

We operate on torch Tensors directly to call the above kernel:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

namespace {
    constexpr int ceil_div(int m, int n) {
        return (m + n - 1) / n;
    }
}

void sgemm_naive(const torch::Tensor &matrix_a, const torch::Tensor &matrix_b,
                 torch::Tensor &output_matrix, float alpha, float beta)
{
    // Validate inputs
    TORCH_CHECK(matrix_a.device().is_cuda(), "Matrix A must be on CUDA device");
    TORCH_CHECK(matrix_b.device().is_cuda(), "Matrix B must be on CUDA device");
    TORCH_CHECK(matrix_a.dtype() == torch::kFloat32, "Matrix A must be float32");
    TORCH_CHECK(matrix_b.dtype() == torch::kFloat32, "Matrix B must be float32");
    TORCH_CHECK(matrix_a.dim() == 2, "Matrix A must be 2D");
    TORCH_CHECK(matrix_b.dim() == 2, "Matrix B must be 2D");

    const int num_rows_a = static_cast<int>(matrix_a.size(0));
    const int num_cols_a = static_cast<int>(matrix_a.size(1));
    const int num_cols_b = static_cast<int>(matrix_b.size(1));

    TORCH_CHECK(matrix_b.size(0) == num_cols_a, "Matrix dimensions must match: A is MxK, B must be KxN");

    TORCH_CHECK(output_matrix.device().is_cuda(), "Matrix C must be on CUDA device");
    TORCH_CHECK(output_matrix.dtype() == torch::kFloat32, "Matrix C must be float32");
    TORCH_CHECK(output_matrix.size(0) == num_rows_a && output_matrix.size(1) == num_cols_b, "Matrix C must be MxN");

    // Get raw device pointers
    const float *d_matrix_a = matrix_a.data_ptr<float>();
    const float *d_matrix_b = matrix_b.data_ptr<float>();
    float *d_output_matrix = output_matrix.data_ptr<float>();

    // Configure kernel launch: 1D blocks with block_size^2 threads (32x32 = 1024 threads per block)
    constexpr uint block_size = 32;
    dim3 block_dim(block_size * block_size);
    dim3 grid_dim(ceil_div(num_rows_a, block_size),
                  ceil_div(num_cols_b, block_size));

    // Launch kernel
    sgemm_naive_kernel<block_size><<<grid_dim, block_dim>>>(
        num_rows_a, num_cols_b, num_cols_a,
        alpha, d_matrix_a, d_matrix_b, beta, d_output_matrix);
}

Performance Analysis

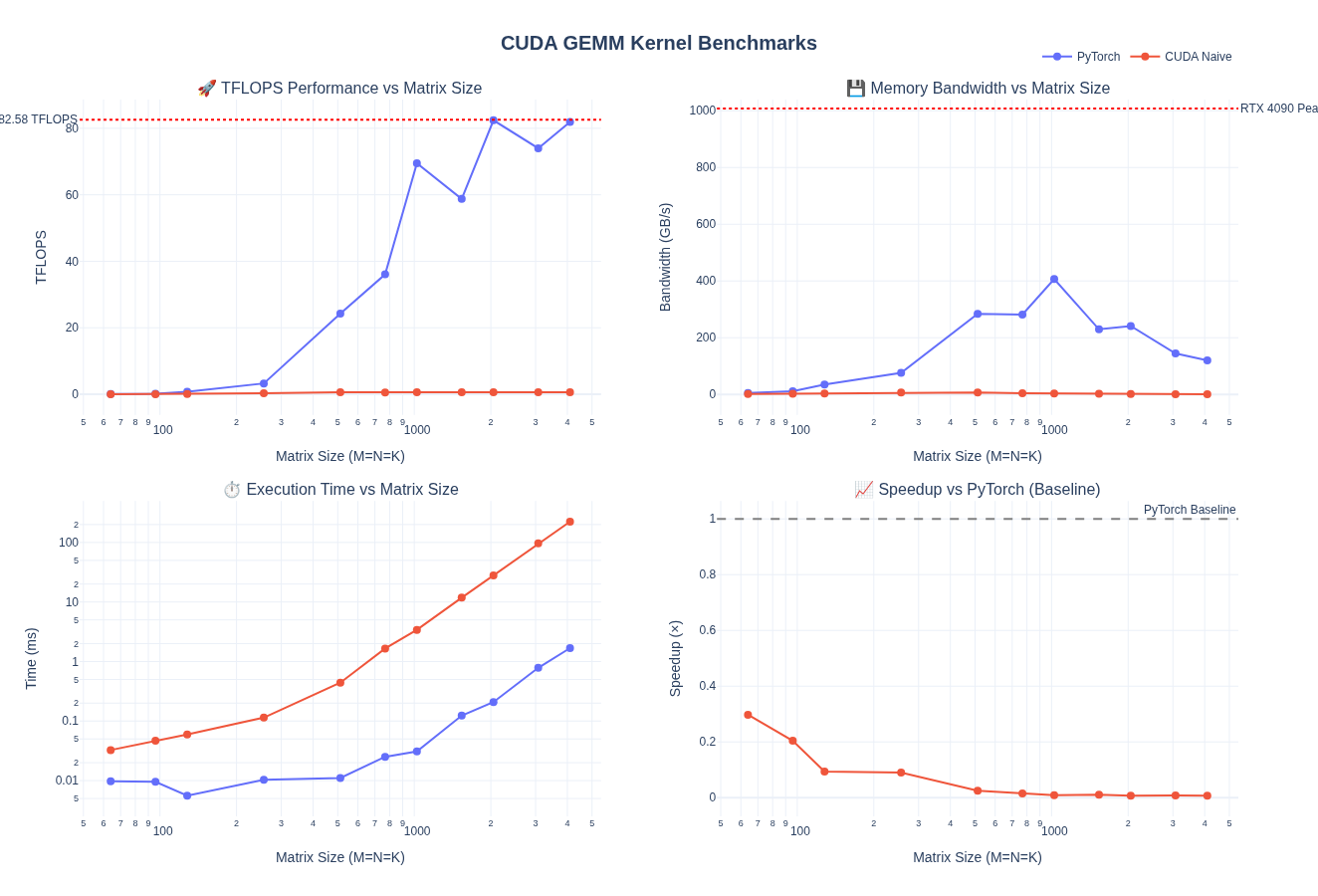
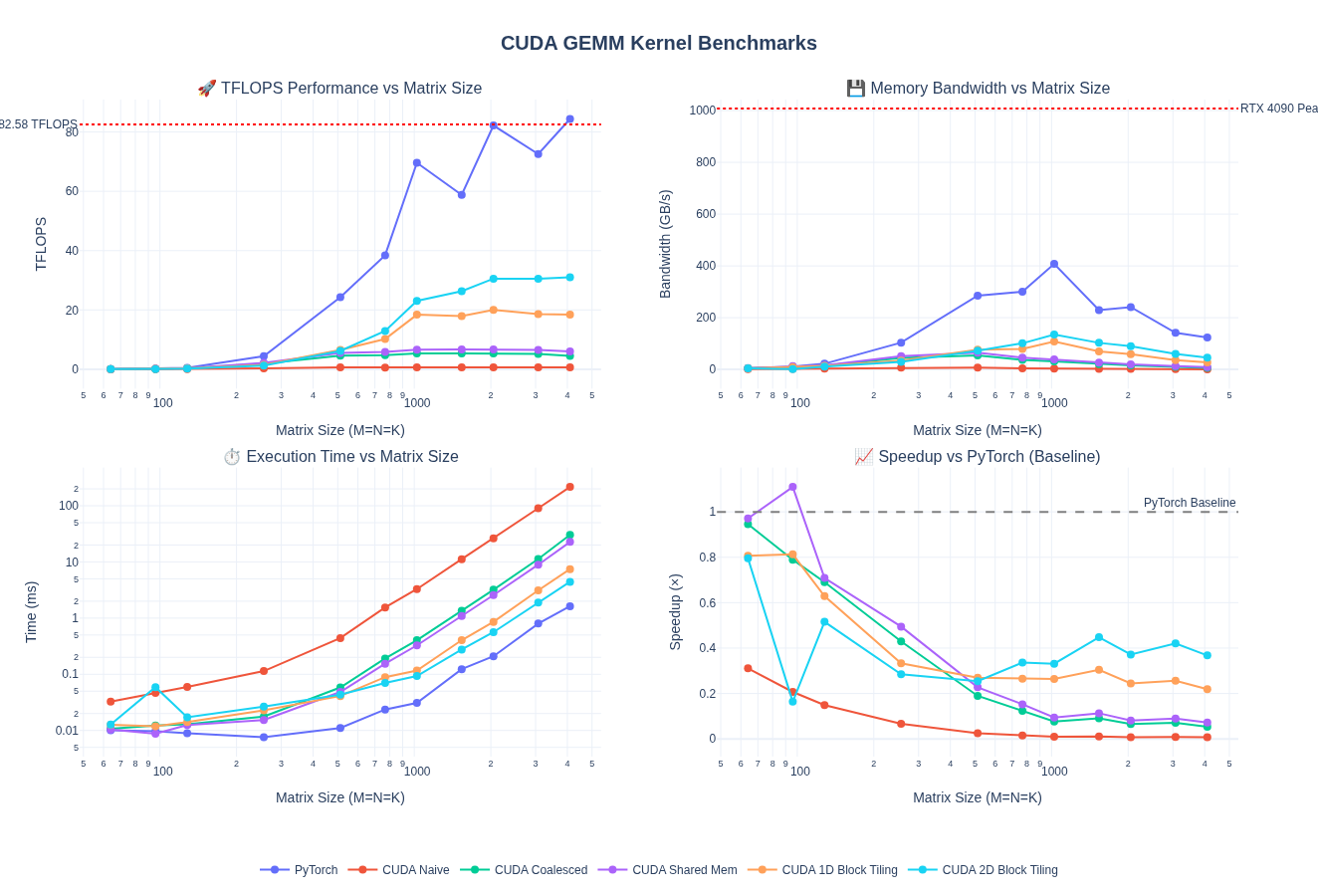
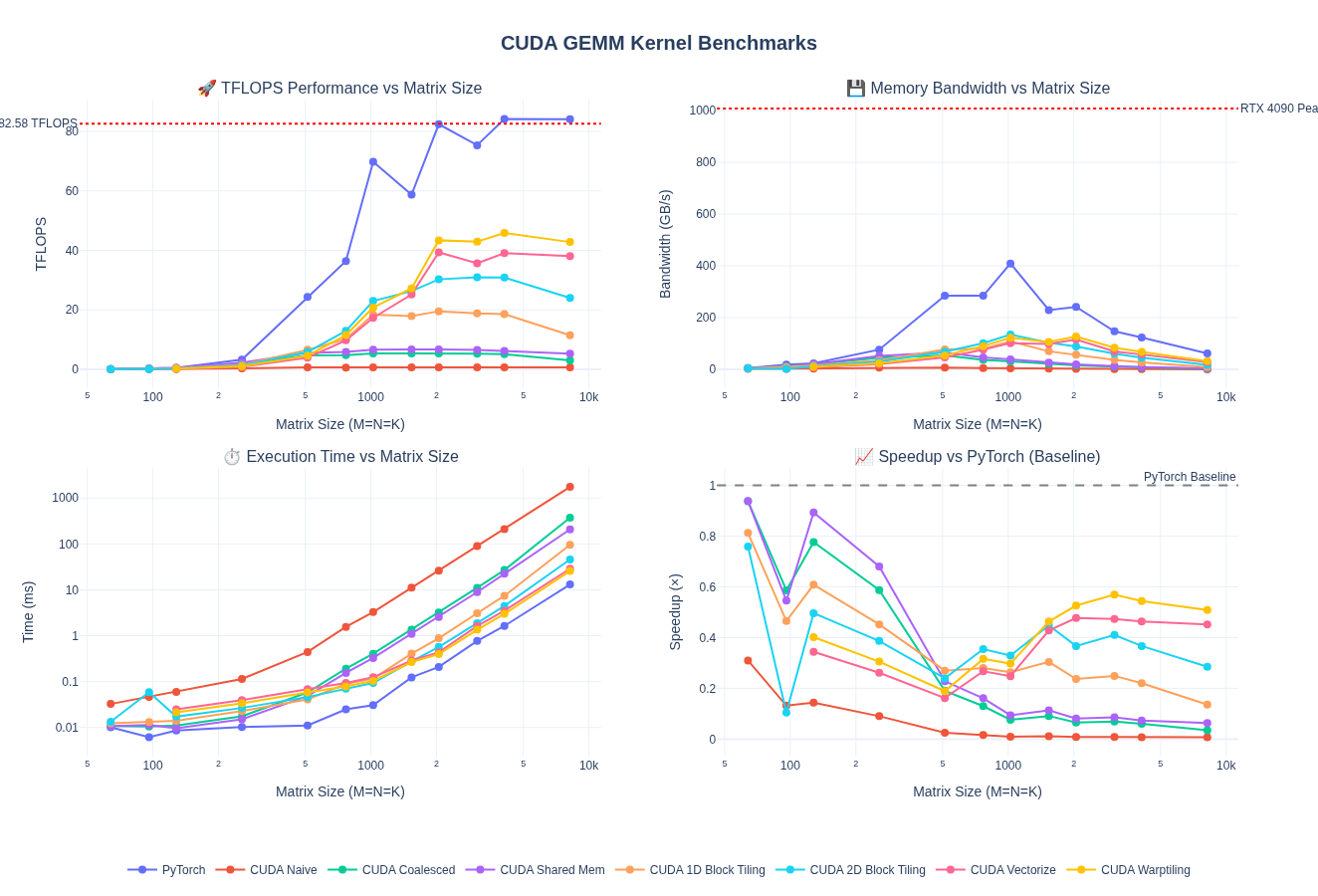
Below are the full benchmark results comparing the naive CUDA kernel against PyTorch’s optimized GEMM implementation across different shapes. As we can see, the naive implementation is significantly slower than PyTorch’s optimized kernel, achieving only ~1% of PyTorch’s performance.

Naive Only

For M = N = K = 4096:

  • The naive CUDA kernel is 133× slower than PyTorch (0.01× speedup)
  • Achieves only 0.76% of PyTorch’s TFLOPS
  • Bandwidth utilization is 133× worse (0.90 GB/s vs 119.97 GB/s)

Global Memory Coalescing

Let’s take a brief digression before we look into why naive kernel is so slow.

Concept

Apart from PMPP book, slides from an NVidia GTC talk is a really good reference to understand the memory hierarchy details and why memory access patterns are the primary consideration when we think about GPU/CUDA performance. For recent architectures, CUTLASS/CUTE documentation is really good reference as well.

Some Basics

To understand memory coalescing, we need to first understand GPU execution hierarchy:

  1. Threads: Individual execution units in your CUDA kernel
  2. Warps: Groups of 32 threads that execute the same instruction simultaneously (SIMT - Single Instruction, Multiple Thread)
  3. Thread Blocks: Logical groupings of threads (up to 1024 threads) that share resources and can synchronize
  4. Streaming Multiprocessors (SMs): The physical processors on the GPU that execute thread blocks

Warps are the fundamental unit of execution such that all 32 threads in a warp execute the same instruction at the same time. Also, when these threads access consecutive memory addresses, the hardware can combine their memory requests into a single transaction. Modern GPU DRAM systems can fetch large contiguous blocks (32B, 64B, or 128B cache lines) in one transaction. Without coalescing, the same 32 accesses could require 32 separate transactions.

In addition, other things to note about SMs include:

  • Each SM has limited resources (registers, shared memory)
  • Multiple thread blocks compete for these resources
  • SMs can switch between warps in a single clock cycle, enabling latency hiding. While one warp waits for memory, another executes
  • GEMM efficiency depends on keeping all warp schedulers busy with coalesced memory access patterns

Why is Naive Kernel Slow?

Let’s add some debug info to see what threads map to what values on A, B

1
2
3
4
5
6
7

+            if (threadIdx.x < 64)
+            {
+                printf("Thread %d ; Warp %d: Multiplying A[%d][%d] * B[%d][%d] = C[%d][%d]\n",
+                       threadIdx.x, threadIdx.x / 32, output_row, k_idx,
+                       k_idx, output_col,
+                       output_row, output_col);
+            }

1
2
3
4
5
6
7
8
9
10

Thread 0 ; Warp 0: Multiplying A[0][0] * B[0][0] = C[0][0]
Thread 1 ; Warp 0: Multiplying A[1][0] * B[0][0] = C[1][0]
...
Thread 30 ; Warp 0: Multiplying A[30][0] * B[0][0] = C[30][0]
Thread 31 ; Warp 0: Multiplying A[31][0] * B[0][0] = C[31][0]
Thread 32 ; Warp 1: Multiplying A[0][0] * B[0][1] = C[0][1]
Thread 33 ; Warp 1: Multiplying A[1][0] * B[0][1] = C[1][1]
...
Thread 62 ; Warp 1: Multiplying A[30][0] * B[0][1] = C[30][1]
Thread 63 ; Warp 1: Multiplying A[31][0] * B[0][1] = C[31][1]

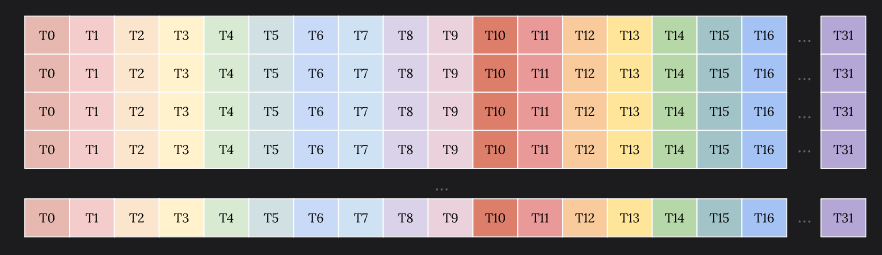
We can see that the naive kernel’s memory access pattern is inefficient. For each thread in a warp, it is accessing A[k][0] values where k is the thread id in a warp. When threads in a warp access scattered memory locations, each access requires a separate memory transaction. It is solvable by memory coalescing such that we restructure the thread-to-output mapping so that threads in the same warp access consecutive memory locations, enabling the hardware to combine multiple accesses into a single transaction.

Problem: Threads access memory in a scattered, non-coalesced pattern.

Turns out the only change we need is to swap % and / across row and col calculations for C.

1
2
3
4
5

    // Map 1D thread ID to 2D output position for coalesced memory access
    // *** KEY CHANGE wrt NAIVE kernel
    const int output_row = blockIdx.x * block_size + (threadIdx.x / block_size);
    const int output_col = blockIdx.y * block_size + (threadIdx.x % block_size);
    // *** KEY CHANGE wrt NAIVE kernel

Memory Access Visualization

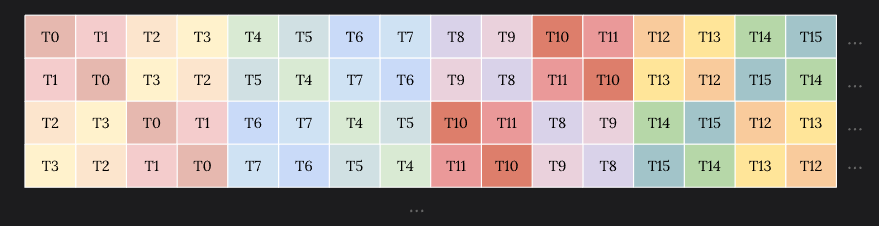
Let’s visualize how the coalesced kernel accesses memory during matrix multiplication. Notice how threads in the same warp now access the same row of matrix A, enabling memory coalescing. We will take a simple example with block_size=4:

Kernel

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

template <const uint block_size>
__global__ void sgemm_global_mem_coalesce_kernel(int num_rows_a, int num_cols_b, int num_cols_a,
                                                 float alpha, const float *matrix_a,
                                                 const float *matrix_b, float beta, float *matrix_c)
{
    // Map 1D thread ID to 2D output position for coalesced memory access
    // *** KEY CHANGE wrt NAIVE kernel
    const int output_row = blockIdx.x * block_size + (threadIdx.x / block_size);
    const int output_col = blockIdx.y * block_size + (threadIdx.x % block_size);
    // *** KEY CHANGE wrt NAIVE kernel

    // Boundary check for non-multiple of block size
    if (output_row < num_rows_a && output_col < num_cols_b)
    {
        float accumulator = 0.0f;
        for (int k_idx = 0; k_idx < num_cols_a; ++k_idx)
        {
            accumulator += matrix_a[output_row * num_cols_a + k_idx] *
                          matrix_b[k_idx * num_cols_b + output_col];
        }
        const int output_idx = output_row * num_cols_b + output_col;
        matrix_c[output_idx] = alpha * accumulator + beta * matrix_c[output_idx];
    }
}

The key change from the naive kernel:

Threads with consecutive threadIdx.x now access consecutive elements in the same row of A, enabling coalescing. I have removed the calling wrapper since it is the same as the last kernel and for brevity.

Performance Analysis

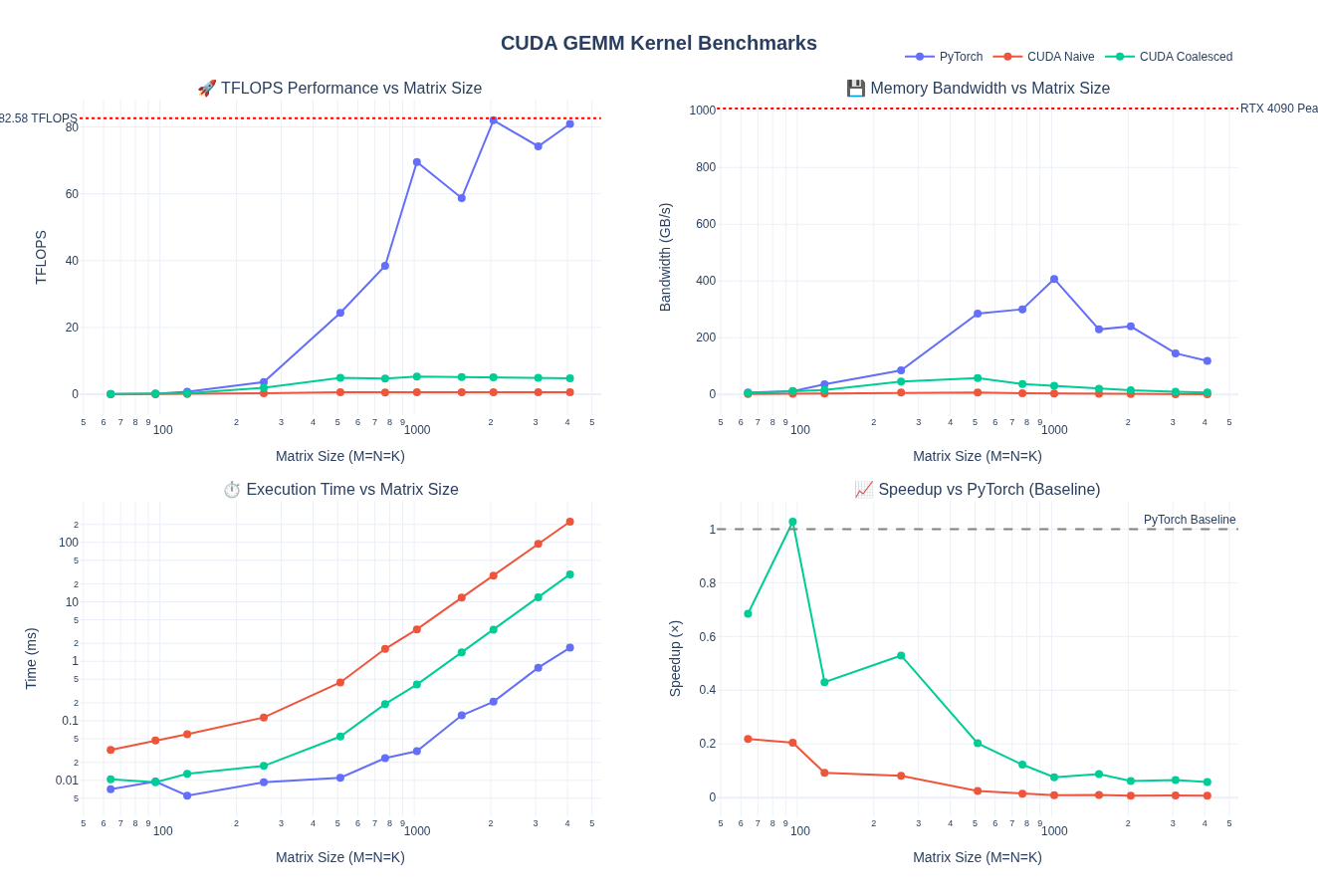
Below are the full benchmark results comparing the naive + coallesced memory access CUDA kernel against PyTorch’s optimized GEMM implementation across different shapes:

Global coalesced

Just like the naive version, we ran a benchmark for N = M = K = 4096 to get the FLOPs and memory bandwidth numbers.

Throughput:

  • 7.63× TFLOPS improvement (0.62 → 4.73 TFLOPS)
  • Still only 5.8% of PyTorch’s performance, but a significant step up

Bandwidth:

  • 7.71× bandwidth improvement (0.90 → 6.94 GB/s)
  • Better memory utilization through coalesced access patterns

We can see that performance improved but still way slower than the pytorch version.

Shared Memory Caching

Concept

Before diving into shared memory optimization, let’s understand the RTX 4090’s memory hierarchy and why shared memory is so critical for performance. Shared memory provides significant bandwidth advantage compared to global memory, since it is on-chip. As a result, latency of loads/stores are at least one order of magnitude better compared to global memory. I could not find any public numbers on the differences though.

Even with coalesced access, both the naive and coalesced kernels repeatedly read the same data from global memory:

  • Each element of matrix $A$ is read $N$ times (once per column of $B$)
  • Each element of matrix $B$ is read $M$ times (once per row of $A$)

Using the Shared Memory

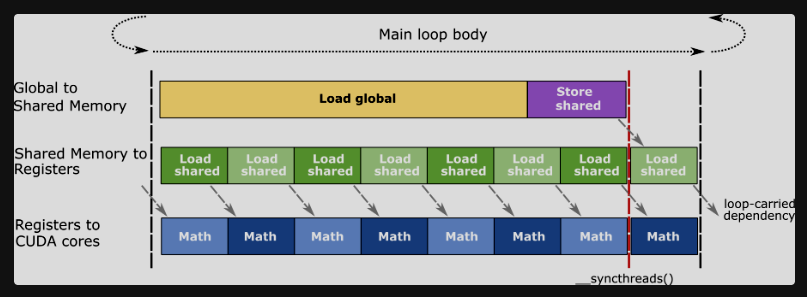
RTX 4090 has 128 KB of shared memory per SM (16MB / 128 SMs) that serves as a fast on-chip cache/shared memory. This shared memory is partitioned among thread blocks (each block gets its own chunk), accessible by all threads within a block. With 128 SMs on the RTX 4090, there’s a total of 16.4 MB of shared memory distributed across the chip. Instead of repeatedly reading the same data from slow global memory, as an optimization strategy, we can load tiles (chunks) of matrices A and B into this fast shared memory, compute partial results using the cached tile data with high reuse across multiple threads, then slide these tiles across the matrices to compute the final result, effectively transforming a bandwidth-bound problem into a compute-bound one. Let’s look at how this works below:

NOTE: We need to synchronize threads after both loading the data into shared memory and also after finishing the tiled matmuls to ensure:

  • All data is loaded before we do the matmul calculations

  • All calculated data is stored back into matrix C before going to next tiles

Kernel

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78

template <const uint block_size>
__global__ void sgemm_shared_mem_kernel(int num_rows_a, int num_cols_b, int num_cols_a,
                                        float alpha, const float *matrix_a,
                                        const float *matrix_b, float beta,
                                        float *matrix_c)
{
    const uint block_row = blockIdx.x;
    const uint block_col = blockIdx.y;

    __shared__ float tile_a[block_size * block_size];
    __shared__ float tile_b[block_size * block_size];

    const uint thread_row = threadIdx.x / block_size;
    const uint thread_col = threadIdx.x % block_size;

    // Calculate global row and column indices for this thread
    const uint global_row = block_row * block_size + thread_row;
    const uint global_col = block_col * block_size + thread_col;

    // Move pointers to the starting position for this block
    matrix_a += block_row * block_size * num_cols_a; // row=block_row, col=0
    matrix_b += block_col * block_size;              // row=0, col=block_col
    matrix_c += block_row * block_size * num_cols_b + block_col * block_size;

    float accumulator = 0.0f;

    // Loop over all tiles along K dimension
    for (int tile_idx = 0; tile_idx < num_cols_a; tile_idx += block_size)
    {
        // Load tile from matrix A into shared memory with bounds checking
        // thread_col is consecutive for coalesced memory access
        if (global_row < num_rows_a && (tile_idx + thread_col) < num_cols_a)
        {
            tile_a[thread_row * block_size + thread_col] =
                matrix_a[thread_row * num_cols_a + thread_col];
        }
        else
        {
            tile_a[thread_row * block_size + thread_col] = 0.0f;
        }

        // Load tile from matrix B into shared memory with bounds checking
        // thread_col is consecutive for coalesced memory access
        if ((tile_idx + thread_row) < num_cols_a && global_col < num_cols_b)
        {
            tile_b[thread_row * block_size + thread_col] =
                matrix_b[thread_row * num_cols_b + thread_col];
        }
        else
        {
            tile_b[thread_row * block_size + thread_col] = 0.0f;
        }

        // Block threads until cache is fully populated
        __syncthreads();

        // Advance pointers to next tile
        matrix_a += block_size;
        matrix_b += block_size * num_cols_b;

        // Compute partial dot product using shared memory
        for (int dot_idx = 0; dot_idx < block_size; ++dot_idx)
        {
            accumulator += tile_a[thread_row * block_size + dot_idx] *
                           tile_b[dot_idx * block_size + thread_col];
        }

        // Sync again to avoid faster threads fetching next block before slower threads finish
        __syncthreads();
    }

    // Write result to global memory with bounds checking: C = α*(A@B)+β*C
    if (global_row < num_rows_a && global_col < num_cols_b)
    {
        matrix_c[thread_row * num_cols_b + thread_col] =
            alpha * accumulator + beta * matrix_c[thread_row * num_cols_b + thread_col];
    }
}

Again, we have removed the caller code since it looks similar to previous kernels

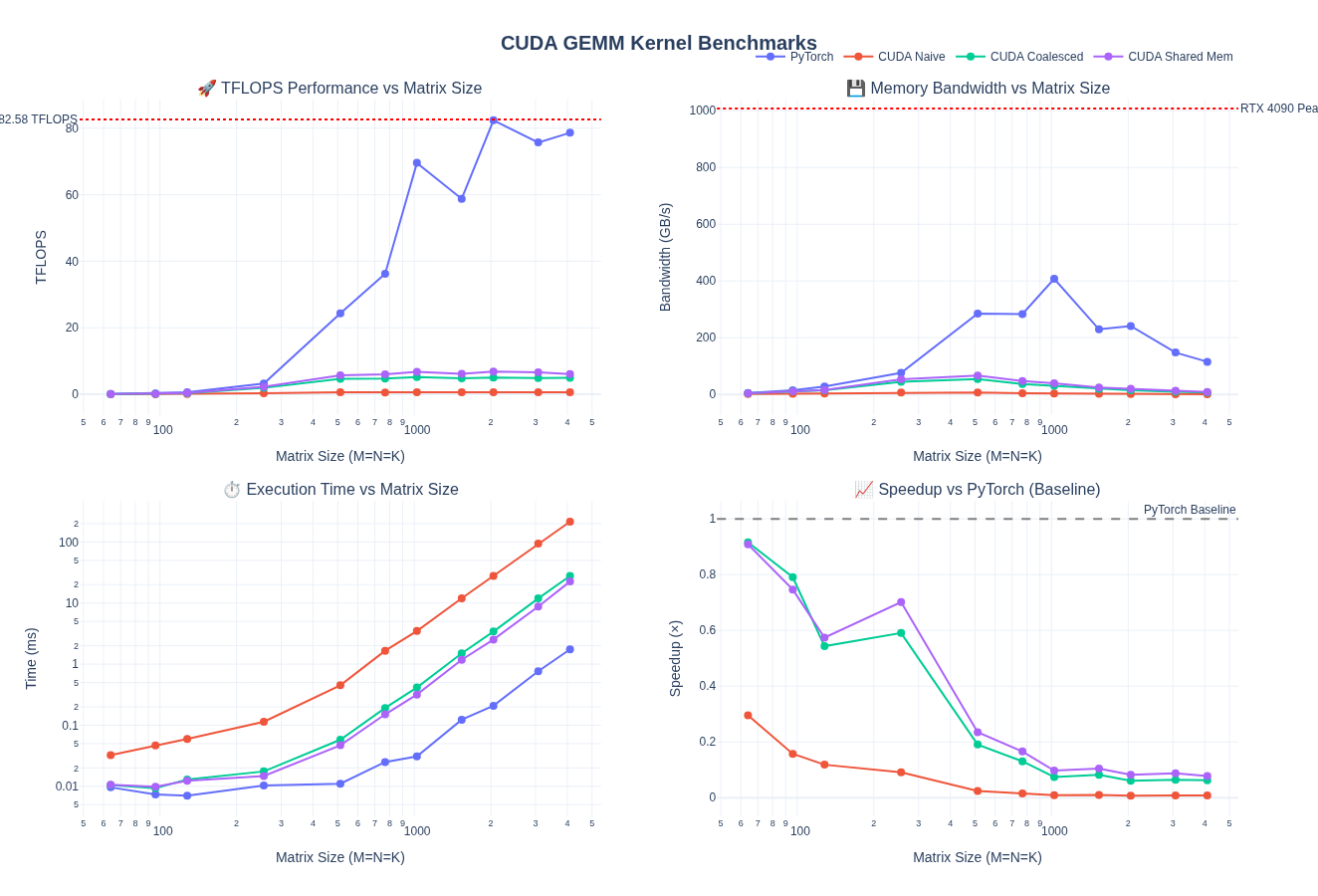
Performance Analysis

Below are all the results from the benchmarking:

Kernel with shared mem

Running the shared memory kernel for M = N = K = 4096:

Performance Improvement:

  • 1.24× TFLOPS improvement over coalesced (4.94 → 6.10 TFLOPS)
  • 1.24× bandwidth improvement (7.23 → 8.94 GB/s)
  • 9.5× faster than naive (0.64 → 6.10 TFLOPS)
  • Still only 7.8% of PyTorch’s performance

Key Insight:

  • Shared memory caching provides modest improvement (~24%) over just coalescing
  • The relatively small gain suggests we’re not yet effectively hiding memory latency

Some improvement but still far behind the baseline performance.

Understanding GPU Occupancy

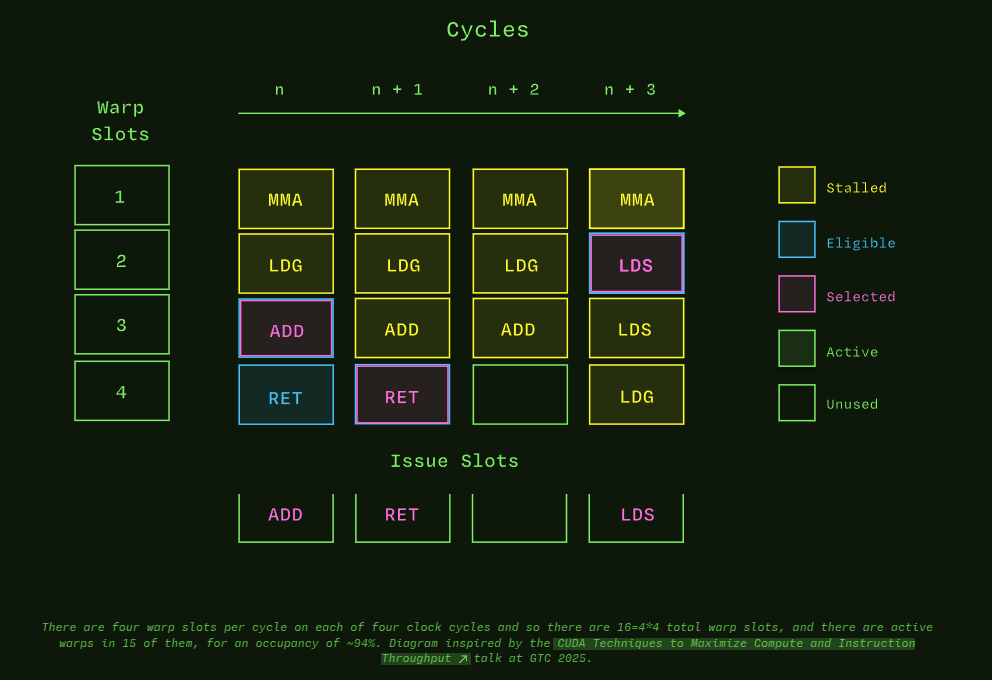
Before diving into more advanced optimizations, we need to understand occupancy, which determines how well we utilize the GPU’s resources.

What is Occupancy?

Occupancy is the ratio of active warps to the maximum number of possible warps per SM:

\[\text{Occupancy} = \frac{\text{Active Warps per SM}}{\text{Maximum Warps per SM}}\]

Here is a really nice diagram and description from Modal GPU Glossary

GPU Glossary occupancy

GPUs hide memory latency through massive parallelism. When one warp waits for memory, the SM immediately switches to execute another warp. Occupancy does not enable performance directly but primarily through latency hiding. Higher occupancy effectively means more warps available for compute and we can hide latency more effectively. If occupancy is low, hardware sits idle waiting for data. However, occupancy is not everything. A kernel with 100% occupancy but poor memory access patterns can still perform poorly since that could lead to lower register/shared memory per thread (covered later). So, it is important to take into account other factors apart from just optimizing for occupancy.

Key Considerations

Now, each thread gets registers from the SM’s register file. More registers per thread implies fewer concurrent threads.

\[\text{Max Threads} = \min\left(\frac{65536 \text{ registers/SM}}{\text{registers per thread}}, 1536\right)\]
Registers/ThreadMax ThreadsActive WarpsOccupancy
321,536 (limited by hardware max)48100%
641,0243266.7%
1285121633.3%

In addition, shared memory is partitioned among thread blocks on the same SM.

\[\text{Max Blocks} = \min\left(\frac{102400 \text{ bytes/SM}}{\text{shared memory per block}}, \underbrace{32}_{\text{hardware limit}}\right)\]

Note: 32 is maximum resident blocks per SM (hardware limit for RTX 4090)

Shared Memory/BlockMax BlocksNotes
0 KB32No shared memory usage
24 KB4Good for moderate tiling
48 KB (max for RTX 4090)2Large tiles, fewer blocks

Lastly, number of threads per block affects how many blocks can fit on an SM and hence affecting occupancy.

Threads/BlockWarps/BlockMax Blocks/SMActive WarpsOccupancy
12841248100%
2568648100%
51216348100%
10243213266.7%

Occupancy for Our Shared Memory Kernel

Let’s analyze our current shared memory kernel:

1
2

constexpr uint BLOCKSIZE = 32;
dim3 block_dim(BLOCKSIZE * BLOCKSIZE);  // 1024 threads per block

Shared memory usage:

1
2
3

__shared__ float tile_a[32 * 32];  // 4 KB
__shared__ float tile_b[32 * 32];  // 4 KB
// Total: 8 KB per block

Occupancy calculation:

  1. Threads per block: 1,024 threads (32 warps)
  2. Blocks per SM (thread limit): $\lfloor 1536 / 1024 \rfloor = 1$ block
  3. Blocks per SM (shared memory limit): $\lfloor 102400 / 8192 \rfloor = 12$ blocks
  4. Blocks per SM (block limit): 32 blocks (max)
  5. Actual blocks per SM: $\min(1, 12, 32) = 1$ block

Active warps: $1 \text{ block} \times 32 \text{ warps/block} = 32 \text{ warps}$

Occupancy: $\frac{32}{48} = 66.7\%$

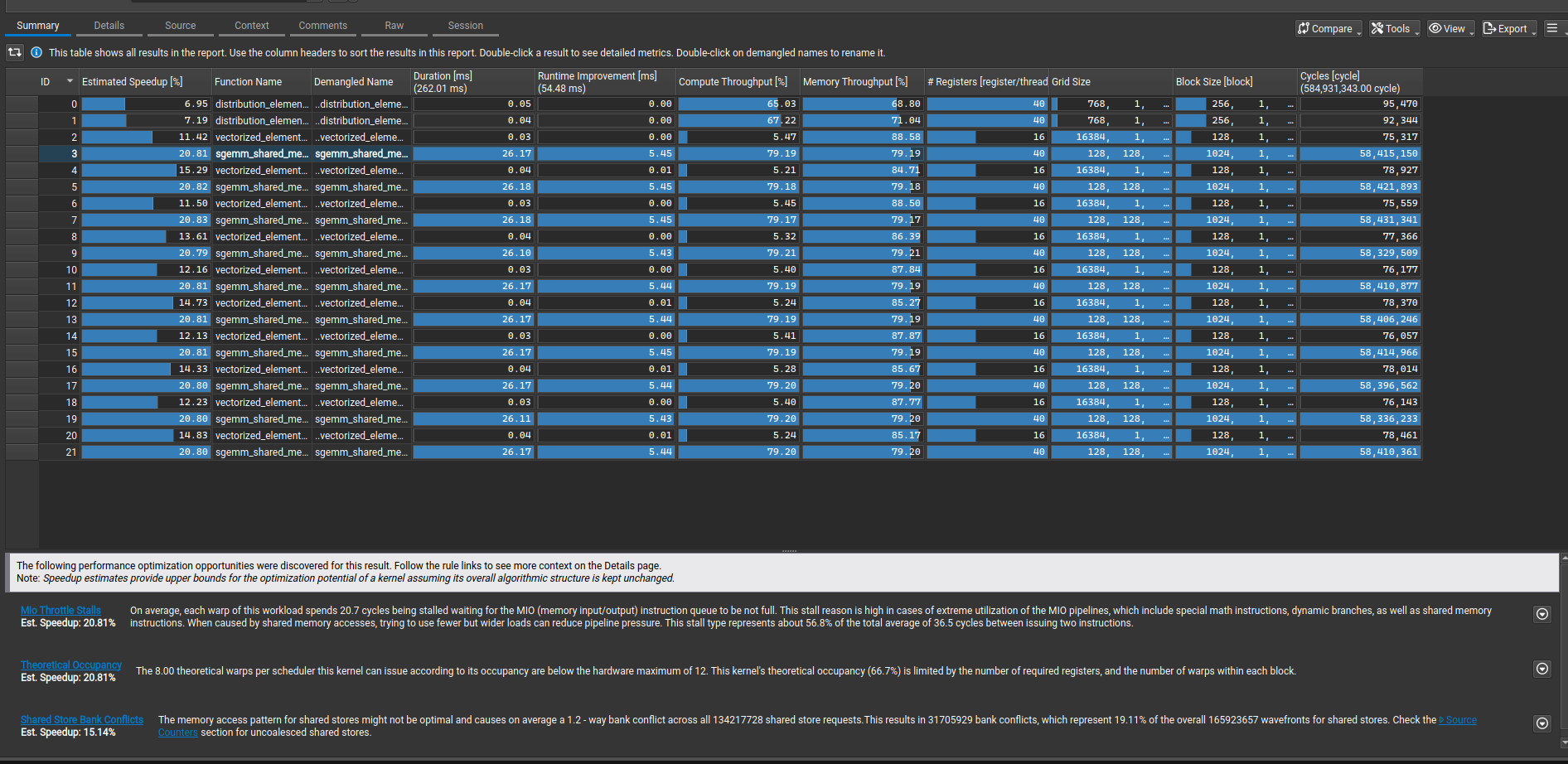
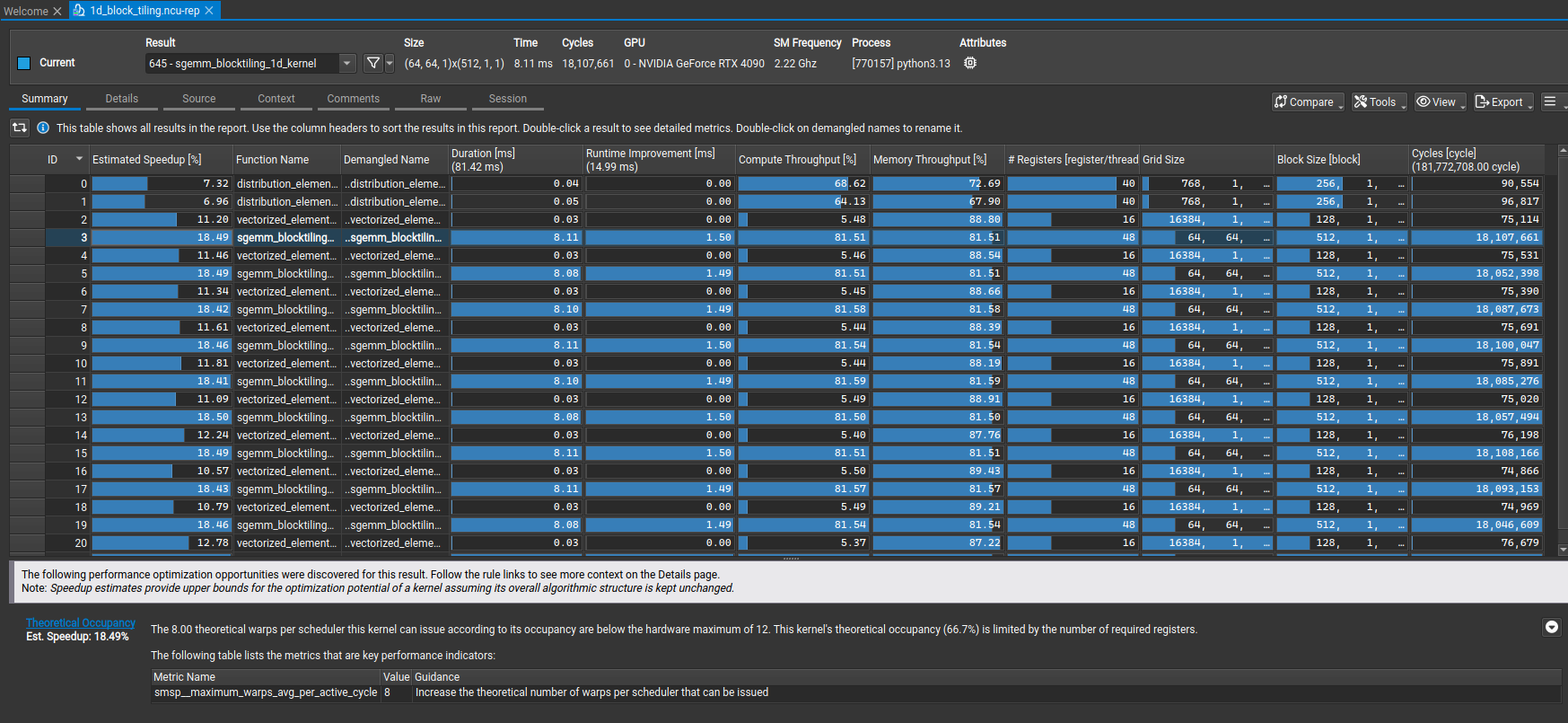
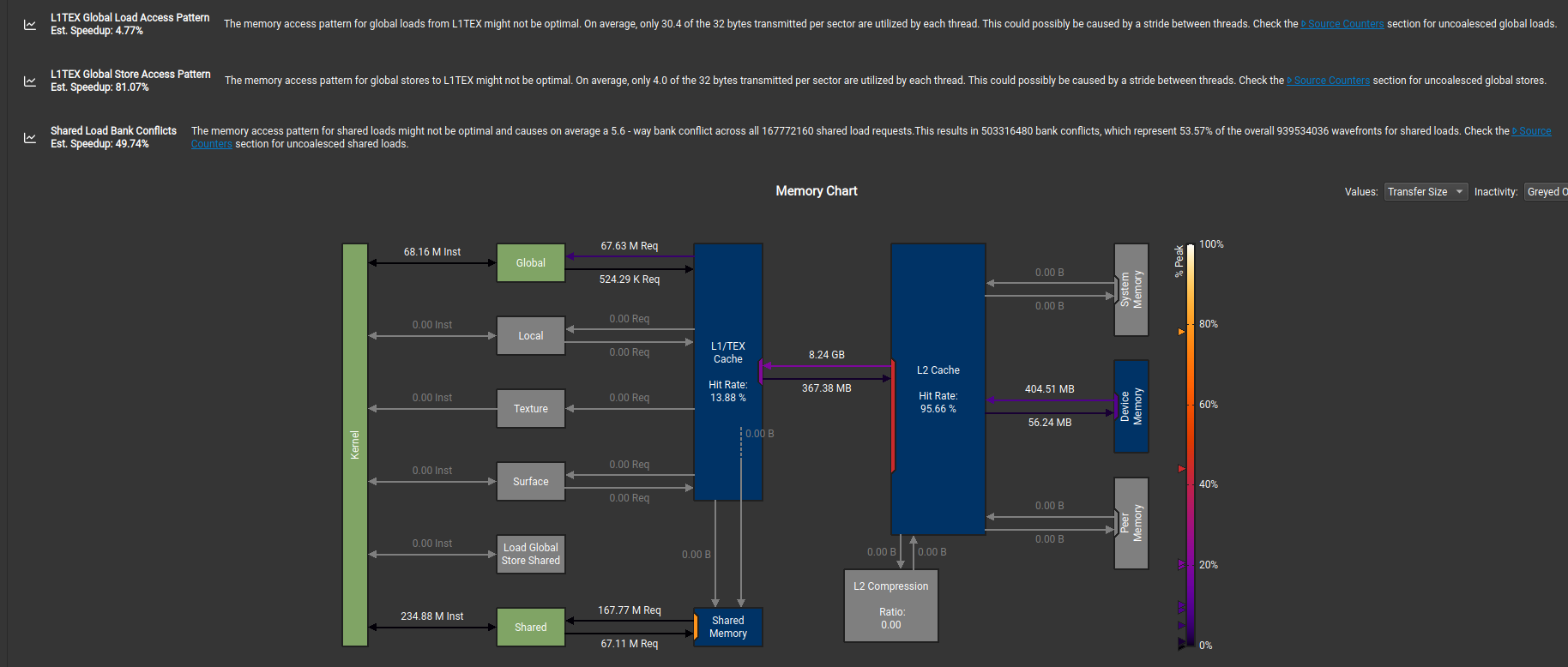
Problem: Our large block size (1,024 threads) limits us to only 1 block per SM, resulting in just 66.7% occupancy. 66.7% occupancy is not necessarily bad but let’s see more details using nsight-compute on how to improve.

Nsight Compute Profiling

First let’s confirm our occupancy calculation and it matches.

shared_mem_occupancy

Now, looking at the summary - it provides some ideas on why the kernel is still slow:

ncu summary shared mem

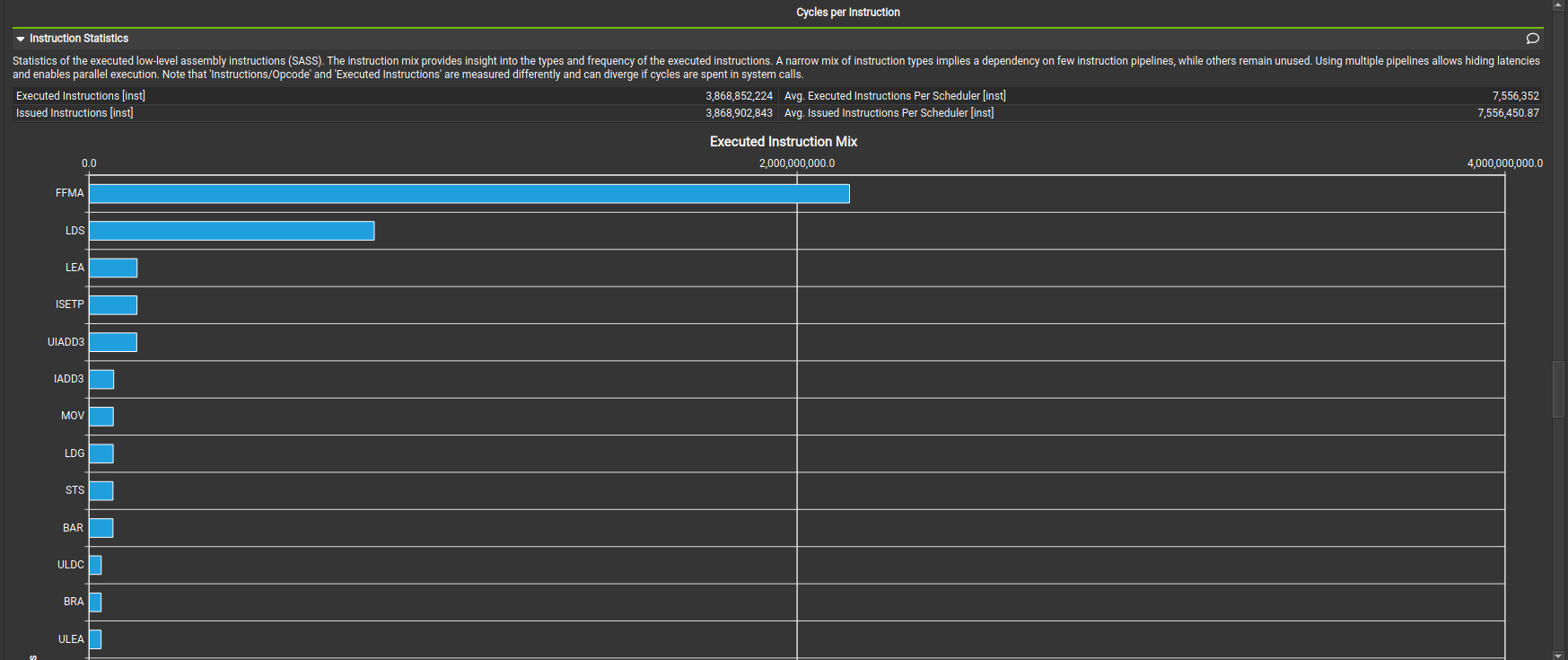
Next, looking at the instruction mix, we can see that LDS dominates the instruction mix, LDS = load within shared memory window, which is not good.

LDS Too much

So, next we will focus on how to reduce the LDS instructions in our kernel.

1D Block Tiling

Concept

In the previous kernel, each thread was computing a single output element of matrix C, meaning each thread needed to load elements from shared memory repeatedly, with memory accesses dominating the execution time.

Next, instead of each thread computing exactly one output element of the tile, each thread computes multiple output elements along one dimension. To support this, we fetch/cache some data from SMEM into registers (for reuse) within each thread, reducing repeated SMEM loads.

In essence, we are trying to improve the arithmetic intensity of the kernel, which effectively means computing more results per thread with the same loaded data i.e. increase FLOPS/byte

To accomplish this, we introduce TM accumulators for TM outputs per thread i.e.

1

float thread_results[TM] = {0.0f};

and later we calculate TM outputs per thread

1
2
3
4
5
6
7
8

for (uint dot_idx = 0; dot_idx < BK; ++dot_idx) {
    float b_tmp = tile_b[dot_idx * BN + thread_col];
    for (uint res_idx = 0; res_idx < TM; ++res_idx) {
        thread_results[res_idx] +=
            tile_a[(thread_row * TM + res_idx) * BK + dot_idx] * b_tmp;
    }
}

Let’s look at a visualization:

Kernel

We now evolve our kernel to introduce paramters that we will need later. We expand on the existing block_size to make them configurable such as BM, BN, BK, etc. They represent the block sizes we are operating on for M, N, and K dimensions. In addition, we add TM as a parameter that determines, how many values calculated per thread! Full listing below:

NOTE: Simon Boehm’s Kernels did not handle bounds check i.e. non-block multiple kernels will be incorrect. I tried to add the bounds check here but we can see that it starts to make the code fairly complex. We will keep the bounds check as long as we can but will drop it later sections to focus on core concepts.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80

template <const int BM, const int BN, const int BK, const int TM>
__global__ void sgemm_blocktiling_1d_kernel(int num_rows_a, int num_cols_b, int num_cols_a,
                                            float alpha, const float *matrix_a,
                                            const float *matrix_b, float beta,
                                            float *matrix_c)
{
    const uint block_row = blockIdx.x;
    const uint block_col = blockIdx.y;

    __shared__ float tile_a[BM * BK];
    __shared__ float tile_b[BK * BN];

    const uint thread_row = threadIdx.x / BN;
    const uint thread_col = threadIdx.x % BN;

    // Calculate global row and column indices for this thread
    const int global_row = block_row * BM + thread_row * TM;
    const int global_col = block_col * BN + thread_col;

    // Move pointers to the starting position for this block
    matrix_a += block_row * BM * num_cols_a;  // row=block_row, col=0
    matrix_b += block_col * BN;               // row=0, col=block_col
    matrix_c += block_row * BM * num_cols_b + block_col * BN;

    // Allocate thread-local cache for results in registerfile
    float thread_results[TM] = {0.0f};

    // Loop over all tiles along K dimension
    for (int tile_idx = 0; tile_idx < num_cols_a; tile_idx += BK)
    {
        // Load tile from matrix A into shared memory with bounds checking
        // Each thread loads one element from A
        const uint a_row = threadIdx.x / BK;
        const uint a_col = threadIdx.x % BK;
        if ((block_row * BM + a_row) < num_rows_a && (tile_idx + a_col) < num_cols_a) {
            tile_a[a_row * BK + a_col] = matrix_a[a_row * num_cols_a + a_col];
        } else {
            tile_a[a_row * BK + a_col] = 0.0f;
        }

        // Load tile from matrix B into shared memory with bounds checking
        // Each thread loads one element from B
        const uint b_row = threadIdx.x / BN;
        const uint b_col = threadIdx.x % BN;
        if ((tile_idx + b_row) < num_cols_a && (block_col * BN + b_col) < num_cols_b) {
            tile_b[b_row * BN + b_col] = matrix_b[b_row * num_cols_b + b_col];
        } else {
            tile_b[b_row * BN + b_col] = 0.0f;
        }

        __syncthreads();

        // Advance pointers to next tile
        matrix_a += BK;
        matrix_b += BK * num_cols_b;

        // Calculate per-thread results
        for (uint dot_idx = 0; dot_idx < BK; ++dot_idx) {
            // We make the dotproduct loop the outside loop, which facilitates
            // reuse of the tile_b entry, which we can cache in a tmp var.
            float b_tmp = tile_b[dot_idx * BN + thread_col];
            for (uint res_idx = 0; res_idx < TM; ++res_idx) {
                thread_results[res_idx] +=
                    tile_a[(thread_row * TM + res_idx) * BK + dot_idx] * b_tmp;
            }
        }

        __syncthreads();
    }

    // Write results to global memory: C = α*(A@B)+β*C
    for (uint res_idx = 0; res_idx < TM; ++res_idx) {
        int row = global_row + res_idx;
        if (row < num_rows_a && global_col < num_cols_b) {
            matrix_c[(thread_row * TM + res_idx) * num_cols_b + thread_col] =
                alpha * thread_results[res_idx] +
                beta * matrix_c[(thread_row * TM + res_idx) * num_cols_b + thread_col];
        }
    }
}

Caller

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

void sgemm_blocktiling_1d(const torch::Tensor &matrix_a, const torch::Tensor &matrix_b,
                          torch::Tensor &output_matrix, float alpha, float beta)
{
    // ... rest of the code is similar 
    // ...
    // Template parameters for kernel
    constexpr int BM = 64;
    constexpr int BN = 64;
    constexpr int BK = 8;
    constexpr int TM = 8;

    // Configure kernel launch
    // Tiling strategy : 
    // - BM x BK from A, BK x BN from B
    // - TM values per thread
    // Number of threads = (BM / TM) * BN = (64 / 8) * 64 = 512 threads per block
    dim3 block_dim((BM / TM) * BN);
    dim3 grid_dim(CEIL_DIV(num_rows_a, BM),
                  CEIL_DIV(num_cols_b, BN));

    // Launch kernel
    sgemm_blocktiling_1d_kernel<BM, BN, BK, TM><<<grid_dim, block_dim>>>(
        num_rows_a, num_cols_b, num_cols_a,
        alpha, d_matrix_a, d_matrix_b, beta, d_output_matrix);
}

Performance Analysis

Let’s look at overall performance across several batch sizes

1D block tiling performance

Performance Improvement:

  • 3.03× TFLOPS improvement over shared memory (6.10 → 18.49 TFLOPS)
  • 3.03× bandwidth improvement (8.94 → 27.08 GB/s)
  • 28.9× faster than naive (0.64 → 18.49 TFLOPS)
  • Achieved 21.8% of PyTorch’s performance (84.62 TFLOPS)

Key Insight:

  • Register-level tiling provides 3× improvement by increasing arithmetic intensity
  • By caching b_tmp in registers and reusing it TM times, we reduce shared memory traffic
  • Each thread now computes TM=8 outputs instead of 1, amortizing memory access costs

Comparison vs Previous Kernels:

KernelTime (ms)TFLOPSvs PyTorchSpeedup over Naive
Naive214.240.640.8%1.0×
Coalesced28.624.805.7%7.5×
Shared Memory22.526.107.2%9.5×
1D Block Tiling7.4318.4921.8%28.9×
PyTorch1.6284.62100%132.1×

NCU profiling

Now, let’s look at how things have changed and confirm our results using ncu!

NCU Summary Stats

NCU summary stats

We can see the warning related to MIO Throttle Stalls and Shared Store Bank Conflicts are gone now

NCU Instruction Mix

NCU execution mix

LDS is no longer the majority of instruction mix.

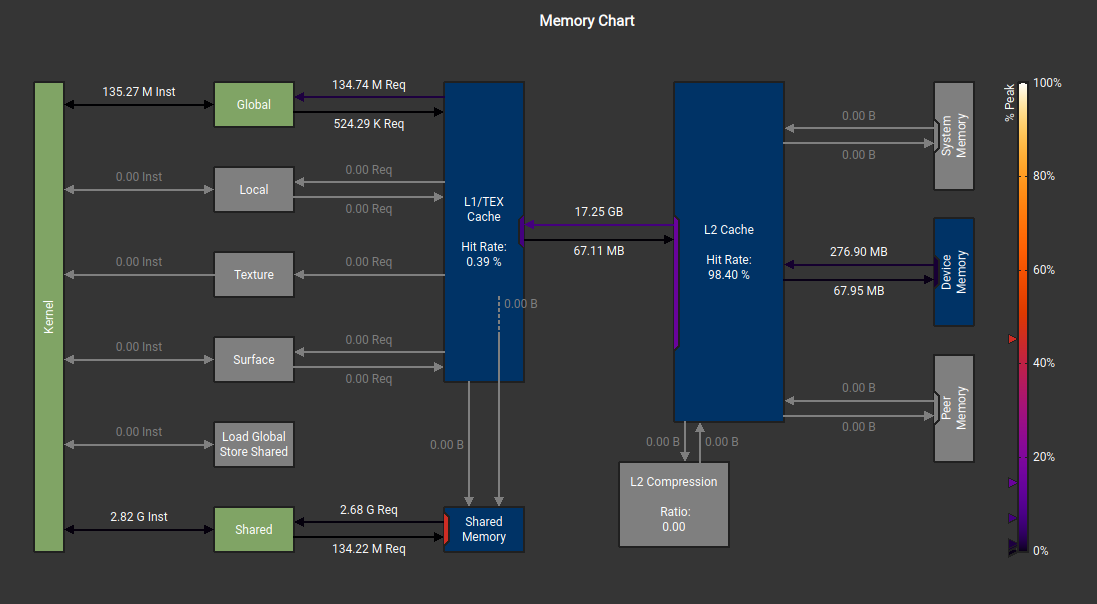
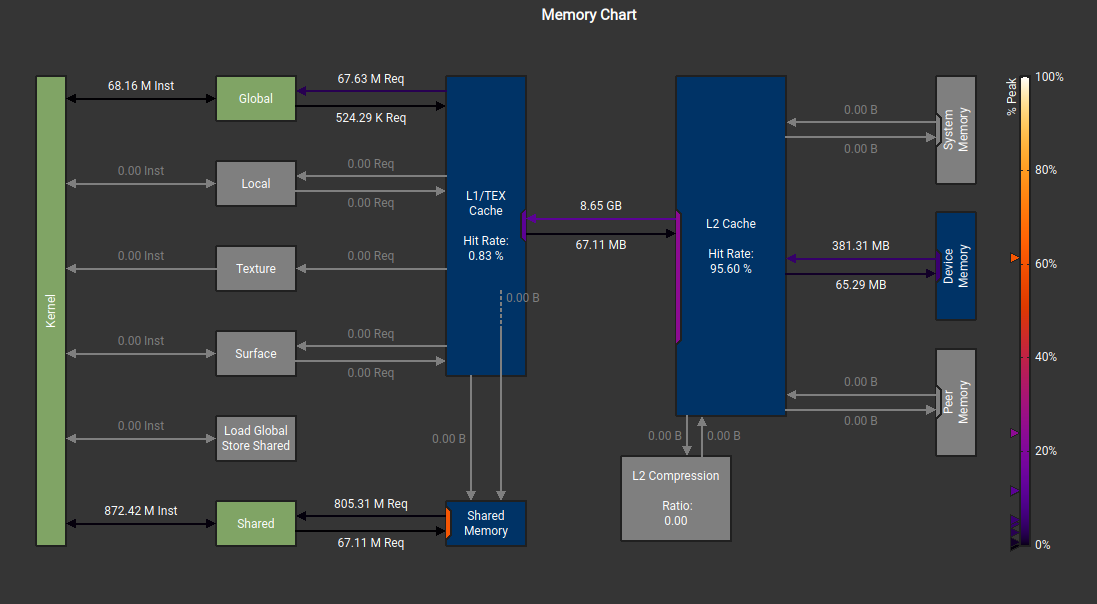
Memory Charts Comparison

The shared memory bandwidth used is also showed in the memory charts. See the comparison below:

Shared Memory Kernel - NCU Memory Profile

Shared Memory Kernel - Higher SMEM traffic, lower throughput

1D Block Tiling Kernel - NCU Memory Profile

1D Block Tiling Kernel - Register caching reduces SMEM traffic, 3× faster

Key takeaway from 1D blocktiling approach is as we calculate more values per thread, we reduce the number of loads/stores per result i.e. increase arithmetic intensity

2D Block Tiling

Concept

2D tiling is a natural extension and enables each thread to compute TM × TN outputs (e.g., 8 × 8 = 64 outputs) instead of just TM outputs (e.g., 8 outputs) in 1D tiling, resulting in TN× more computation per thread with more register usage. Of course, we would need to keep within the register memory bounds but this is how we can increase arithmetic intensity further by reusing shared memory. This creates bidirectional register reuse:

  • Each value from A (loaded into register_m[TM]) is reused across TN computations
  • Each value from B (loaded into register_n[TN]) is reused across TM computations
  • This forms an “outer product” pattern at the register level

In the code, I implemented two separate kernels such that a Main Kernel (No Bounds Checking) handles all interior blocks where every memory access is guaranteed to be in-bounds, helping with zero thread divergence since all threads can execute the same logic. An Edge Kernel (With Bounds Checking) handles boundary blocks at the right edge, bottom edge, and corner. This structures the code well but the code is starting to look fairly complex at this point.

Kernel

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89

template <const int BM, const int BN, const int BK, const int TM, const int TN>
__global__ void sgemm_blocktiling_2d_kernel(int num_rows_a, int num_cols_b, int num_cols_a,
                                            float alpha, const float *matrix_a,
                                            const float *matrix_b, float beta,
                                            float *matrix_c)
{
    const uint block_row = blockIdx.x;
    const uint block_col = blockIdx.y;

    __shared__ float tile_a[BM * BK];
    __shared__ float tile_b[BK * BN];

    const uint thread_row = threadIdx.x / (BN / TN);
    const uint thread_col = threadIdx.x % (BN / TN);
    const uint num_threads = (BM / TM) * (BN / TN);

    matrix_a += block_row * BM * num_cols_a;
    matrix_b += block_col * BN;
    matrix_c += block_row * BM * num_cols_b + block_col * BN;

    float thread_results[TM * TN] = {0.0f};
    float register_m[TM] = {0.0f};
    float register_n[TN] = {0.0f};

    for (uint block_k_idx = 0; block_k_idx < num_cols_a; block_k_idx += BK)
    {
#pragma unroll
        for (uint load_offset = 0; load_offset < BM * BK; load_offset += num_threads)
        {
            uint load_idx = threadIdx.x + load_offset;
            uint a_row = load_idx / BK;
            uint a_col = load_idx % BK;
            tile_a[load_idx] = matrix_a[a_row * num_cols_a + a_col];
        }

#pragma unroll
        for (uint load_offset = 0; load_offset < BK * BN; load_offset += num_threads)
        {
            uint load_idx = threadIdx.x + load_offset;
            uint b_row = load_idx / BN;
            uint b_col = load_idx % BN;
            tile_b[load_idx] = matrix_b[b_row * num_cols_b + b_col];
        }

        __syncthreads();

        matrix_a += BK;
        matrix_b += BK * num_cols_b;

        for (uint dot_idx = 0; dot_idx < BK; ++dot_idx)
        {
            for (uint i = 0; i < TM; ++i)
            {
                register_m[i] = tile_a[(thread_row * TM + i) * BK + dot_idx];
            }

            for (uint i = 0; i < TN; ++i)
            {
                register_n[i] = tile_b[dot_idx * BN + thread_col * TN + i];
            }

            // Each thread calculates TM x TN outputs
            for (uint res_idx_m = 0; res_idx_m < TM; ++res_idx_m)
            {
                for (uint res_idx_n = 0; res_idx_n < TN; ++res_idx_n)
                {
                    thread_results[res_idx_m * TN + res_idx_n] +=
                        register_m[res_idx_m] * register_n[res_idx_n];
                }
            }
        }

        __syncthreads();
    }

#pragma unroll
    for (uint res_idx_m = 0; res_idx_m < TM; ++res_idx_m)
    {
#pragma unroll
        for (uint res_idx_n = 0; res_idx_n < TN; ++res_idx_n)
        {
            const uint c_idx = (thread_row * TM + res_idx_m) * num_cols_b +
                               (thread_col * TN + res_idx_n);
            matrix_c[c_idx] = alpha * thread_results[res_idx_m * TN + res_idx_n] +
                              beta * matrix_c[c_idx];
        }
    }
}

You will notice we are using #pragma unroll directives in the code. What does #pragma unroll do?

It is a compiler optimization technique that can, for example, replace a piece of code like

1
2

for (int i = 0; i < 5; i++ )
    b[i] = i;

with

1
2
3
4
5

b[0] = 0;
b[1] = 1;
b[2] = 2;
b[3] = 3;
b[4] = 4;

by putting #pragma unroll directive right before the loop. I mostly used it since I found it in bunch of other example kernels I saw.

Caller

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

void sgemm_blocktiling_2d(const torch::Tensor &matrix_a, const torch::Tensor &matrix_b,
                          torch::Tensor &output_matrix, float alpha, float beta)
{
    // ... same as previous kernels
    constexpr int BM = 64;
    constexpr int BN = 64;
    constexpr int BK = 8;
    constexpr int TM = 8;
    constexpr int TN = 8;

    // Number of threads launches as part of the block
    // (64 / 8) * (64 / 8) = 64
    dim3 block_dim((BM / TM) * (BN / TN));

    const int num_blocks_m = ceil_div(num_rows_a, BM);
    const int num_blocks_n = ceil_div(num_cols_b, BN);
    const int main_blocks_m = num_rows_a / BM;
    const int main_blocks_n = num_cols_b / BN;

    if (main_blocks_m > 0 && main_blocks_n > 0)
    {
        dim3 main_grid(main_blocks_m, main_blocks_n);
        sgemm_blocktiling_2d_kernel<BM, BN, BK, TM, TN><<<main_grid, block_dim>>>(
            num_rows_a, num_cols_b, num_cols_a,
            alpha, d_matrix_a, d_matrix_b, beta, d_output_matrix);
    }

    // ... handle edge kernels
}

Performance Analysis

Looking at the benchmark results for 4096×4096 matrices, the 2D block tiling kernel shows further performance gains:

Performance Improvement:

  • 1.66× TFLOPS improvement over 1D block tiling (18.40 → 30.55 TFLOPS)
  • 1.66× bandwidth improvement (26.96 → 44.75 GB/s)
  • 38.7% of PyTorch’s performance (79.00 TFLOPS)
  • 46.9× faster than naive (0.652 → 30.55 TFLOPS)

Comparison vs Previous Kernels (4096×4096):

KernelTime (ms)TFLOPSBandwidth (GB/s)vs PyTorchSpeedup over Naive
Naive210.750.650.960.8%1.0×
Coalesced26.965.107.476.5%7.8×
Shared Memory22.676.068.887.7%9.3×
1D Block Tiling7.4718.4026.9623.3%28.2×
2D Block Tiling4.5030.5544.7538.7%46.9×
PyTorch1.7479.00115.73100%121.2×

Performance Across Matrix Sizes

2D block tiling performance

As next steps, when we check our kernel in Nsight compute, we get more pointers to improve performance:

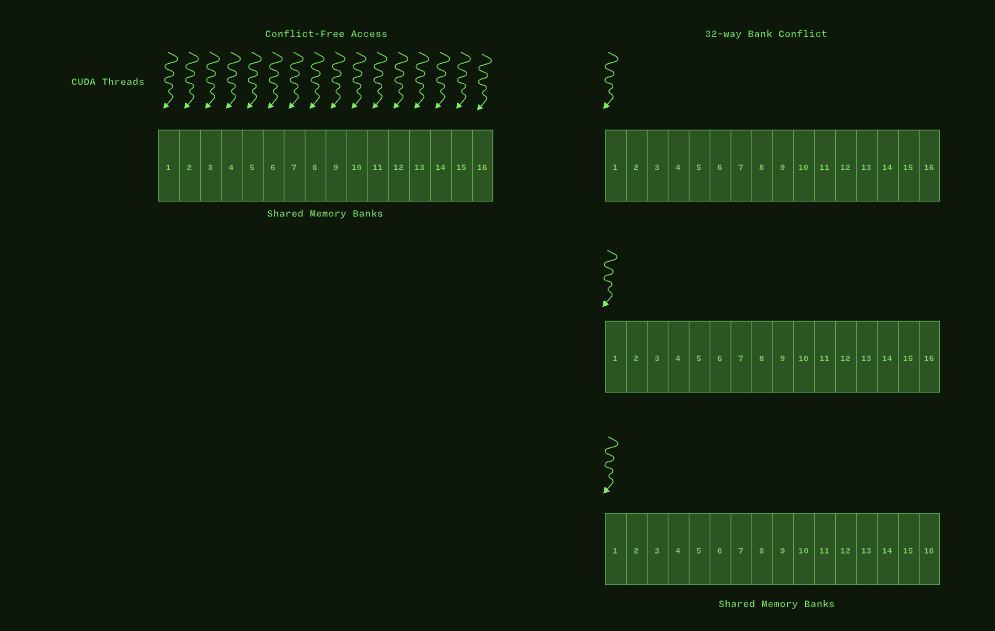
  • L1TEX Global Store Access Pattern: The memory access pattern for global stores to L1TEX might not be optimal. On average, only 4.0 of the 32 bytes transmitted per sector are utilized by each thread. This could possibly be caused by a stride between threads. Check the Source Counters section for uncoalesced global stores.
  • Shared Load Bank Conflicts: The memory access pattern for shared loads might not be optimal and causes on average a 5.6 - way bank conflict across all 167772160 shared load requests.This results in 503316480 bank conflicts, which represent 53.57% of the overall 939534036 wavefronts for shared loads. Check the Source Counters section for uncoalesced shared loads.
  • Uncoalesced Shared Accesses: This kernel has uncoalesced shared accesses resulting in a total of 369098752 excessive wavefronts (37% of the total 1006632960 wavefronts). Check the L1 Wavefronts Shared Excessive table for the primary source locations. The CUDA Best Practices Guide has an example on optimizing shared memory accesses.

NCU After 2D Tiling

Vectorized Memory Access

Concept

As we have realized already, GEMMs are bottlenecked by memory transfer speed. Another optimization that can increase effective bandwidth utilization is to use vectorized memory operations.

CUDA provides built-in vector types (float2, float4, int2, int4) that enable loading or storing multiple values in a single instruction. Instead of issuing four separate 32-bit loads, a single float4 load can fetch 128 bits (16 bytes) at once.

Good reference for Vectorized Memory Access for Performance: CUDA Pro Tip: Increase Performance with Vectorized Memory Access

In our 2D block tiling kernel, each thread loads elements from shared memory to registers. Currently, these loads happen as individual 32-bit transactions:

1
2
3
4
5
6
7
8
9
10
11
12
13
14

// Current approach: scalar loads
for (uint dot_idx = 0; dot_idx < BK; ++dot_idx) {
    // Load TM elements from tile_a into registers
    for (uint i = 0; i < TM; ++i) {
        register_m[i] = tile_a[(thread_row * TM + i) * BK + dot_idx];  // 32-bit load
    }

    // Load TN elements from tile_b into registers
    for (uint i = 0; i < TN; ++i) {
        register_n[i] = tile_b[dot_idx * BN + thread_col * TN + i];  // 32-bit load
    }

    // ... compute outer product
}

If TM=8, we’re issuing 8 separate load instructions. With vectorization, we can combine these into 2 loads of float4. Let’s see how this works:

1
2
3
4
5
6
7
8
9
10
11
12
13
14

// Vectorized approach: load 4 elements at once
for (uint dot_idx = 0; dot_idx < BK; ++dot_idx) {
    // Load 8 elements from tile_a using 2× float4 instead of 8× float
    *reinterpret_cast<float4*>(&register_m[0]) =
        *reinterpret_cast<const float4*>(&tile_a[(thread_row * TM) * BK + dot_idx]);
    *reinterpret_cast<float4*>(&register_m[4]) =
        *reinterpret_cast<const float4*>(&tile_a[(thread_row * TM + 4) * BK + dot_idx]);

    // Load 8 elements from tile_b using 2× float4 instead of 8× float
    *reinterpret_cast<float4*>(&register_n[0]) =
        *reinterpret_cast<const float4*>(&tile_b[dot_idx * BN + thread_col * TN]);
    *reinterpret_cast<float4*>(&register_n[4]) =
        *reinterpret_cast<const float4*>(&tile_b[dot_idx * BN + thread_col * TN + 4]);
}

When you load a float4, the compiler emits a 128-bit vectorized instruction (LDG.E.128) instead of four 32-bit loads (LDG.E):

Load TypeSizeInstructionElementsInstructions Needed
float32 bitsLDG.E14 (for 4 elements)
float264 bitsLDG.E.6422 (for 4 elements)
float4128 bitsLDG.E.12841 (for 4 elements)

Vectorized loads only work efficiently when data is properly aligned to vector size e.g. 16 bytes for float4 and access patterns respect alignment boundaries

1
2
3
4
5
6
7
8
9
10

/*
- 1 vectorized load instruction
- Guaranteed single 128-bit memory transaction
- Hardware-enforced coalescing
*/
float4 vec = *reinterpret_cast<const float4*>(&A[i]);  // LDG.E.128 (128-bit)
float a = vec.x;
float b = vec.y;
float c = vec.z;
float d = vec.w;

Trade-Offs: Vectorized float4 loads reduce memory transactions but increase register pressure (potentially lowering occupancy), require tail handling for non-divisible sizes, and may not benefit shared memory accesses with strided layouts without restructuring.

NOTE: In our case, we will skip the tail handling and assume the inputs are aligned to the block sizes used in the kernel just to simplify the kernel

Kernel

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101

template <const int BM, const int BN, const int BK, const int TM, const int TN>
__global__ void sgemm_vectorize_kernel(int num_rows_a, int num_cols_b, int num_cols_a,
                                       float alpha, const float *matrix_a,
                                       const float *matrix_b, float beta,
                                       float *matrix_c)
{
    const uint block_row = blockIdx.y;
    const uint block_col = blockIdx.x;

    // Thread indices for computing output tile
    const uint thread_col = threadIdx.x % (BN / TN);
    const uint thread_row = threadIdx.x / (BN / TN);

    // Shared memory tiles - stored in column-major for A to enable coalescing
    __shared__ float tile_a[BM * BK];
    __shared__ float tile_b[BK * BN];

    // Position matrix pointers at the start of this block's tile
    matrix_a += block_row * BM * num_cols_a;
    matrix_b += block_col * BN;
    matrix_c += block_row * BM * num_cols_b + block_col * BN;

    // Thread indices for vectorized loading
    // Load 4 floats at a time using float4
    const uint inner_row_a = threadIdx.x / (BK / 4);
    const uint inner_col_a = threadIdx.x % (BK / 4);
    const uint inner_row_b = threadIdx.x / (BN / 4);
    const uint inner_col_b = threadIdx.x % (BN / 4);

    // Allocate register storage
    float thread_results[TM * TN] = {0.0f};
    float register_m[TM] = {0.0f};
    float register_n[TN] = {0.0f};

    // Outer loop over K dimension
    for (uint block_k_idx = 0; block_k_idx < num_cols_a; block_k_idx += BK) {

        // Load tile_a using float4 vectorized loads
        // Store in transposed layout: tile_a[col][row] for coalesced shared memory access
        float4 tmp_a = reinterpret_cast<const float4*>(
            &matrix_a[inner_row_a * num_cols_a + inner_col_a * 4])[0];
        tile_a[(inner_col_a * 4 + 0) * BM + inner_row_a] = tmp_a.x;
        tile_a[(inner_col_a * 4 + 1) * BM + inner_row_a] = tmp_a.y;
        tile_a[(inner_col_a * 4 + 2) * BM + inner_row_a] = tmp_a.z;
        tile_a[(inner_col_a * 4 + 3) * BM + inner_row_a] = tmp_a.w;

        // Load tile_b using float4 vectorized loads
        // Store in row-major layout: tile_b[row][col]
        float4 tmp_b = reinterpret_cast<const float4*>(
            &matrix_b[inner_row_b * num_cols_b + inner_col_b * 4])[0];
        tile_b[inner_row_b * BN + inner_col_b * 4 + 0] = tmp_b.x;
        tile_b[inner_row_b * BN + inner_col_b * 4 + 1] = tmp_b.y;
        tile_b[inner_row_b * BN + inner_col_b * 4 + 2] = tmp_b.z;
        tile_b[inner_row_b * BN + inner_col_b * 4 + 3] = tmp_b.w;

        __syncthreads();

        // Advance pointers for next tile
        matrix_a += BK;
        matrix_b += BK * num_cols_b;

        for (uint dot_idx = 0; dot_idx < BK; ++dot_idx) {
            // Load TM elements from tile_a (transposed layout)
            #pragma unroll
            for (uint i = 0; i < TM; ++i) {
                register_m[i] = tile_a[dot_idx * BM + thread_row * TM + i];
            }

            // Load TN elements from tile_b
            #pragma unroll
            for (uint i = 0; i < TN; ++i) {
                register_n[i] = tile_b[dot_idx * BN + thread_col * TN + i];
            }

            // Outer product accumulation
            #pragma unroll
            for (uint res_idx_m = 0; res_idx_m < TM; ++res_idx_m) {
                #pragma unroll
                for (uint res_idx_n = 0; res_idx_n < TN; ++res_idx_n) {
                    thread_results[res_idx_m * TN + res_idx_n] +=
                        register_m[res_idx_m] * register_n[res_idx_n];
                }
            }
        }

        __syncthreads();
    }

    // Write results with alpha/beta scaling
    #pragma unroll
    for (uint res_idx_m = 0; res_idx_m < TM; ++res_idx_m) {
        #pragma unroll
        for (uint res_idx_n = 0; res_idx_n < TN; ++res_idx_n) {
            const uint c_idx = (thread_row * TM + res_idx_m) * num_cols_b +
                               (thread_col * TN + res_idx_n);
            matrix_c[c_idx] = alpha * thread_results[res_idx_m * TN + res_idx_n] +
                              beta * matrix_c[c_idx];
        }
    }
}

We have removed the caller code since that is unchanged

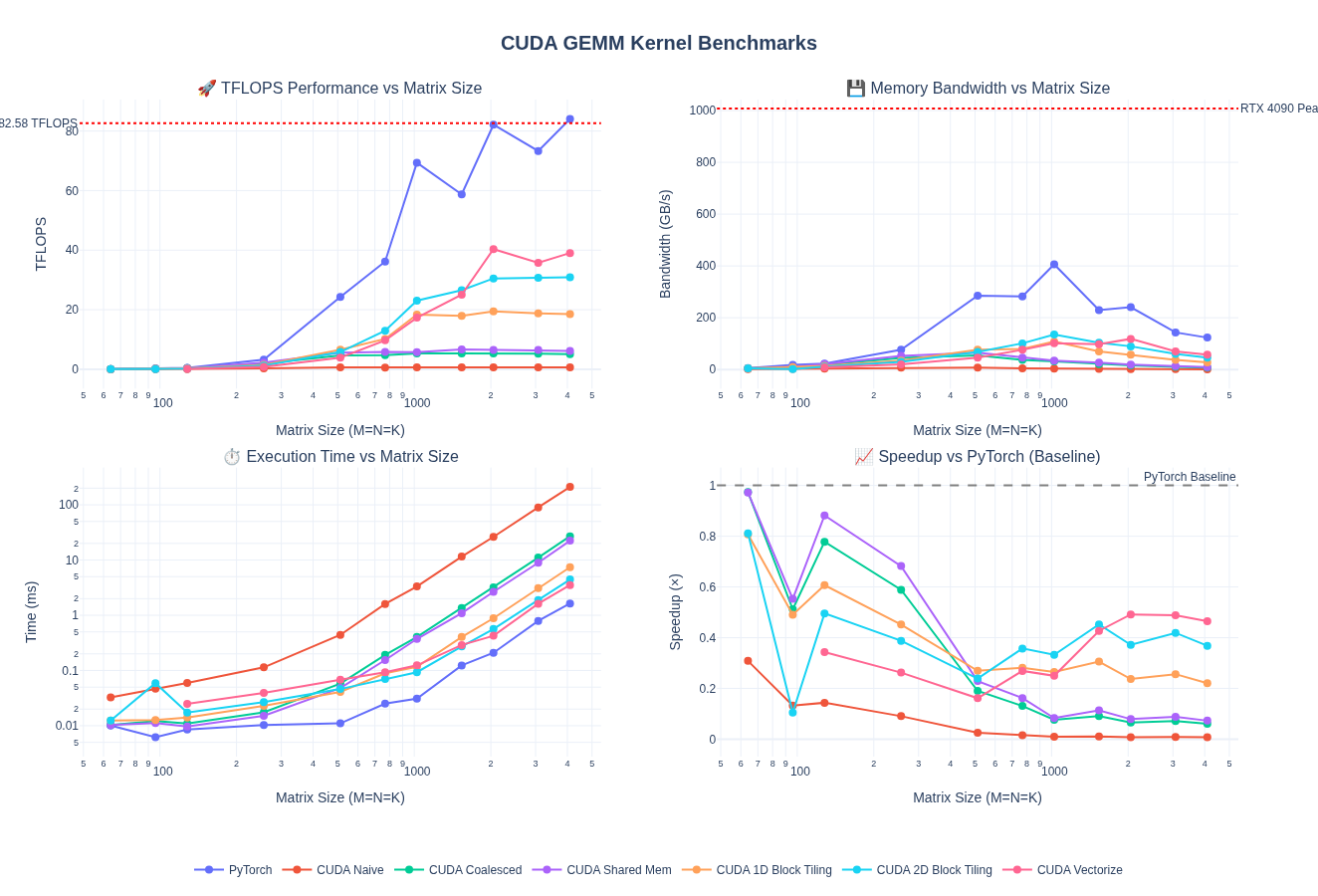
Performance Analysis

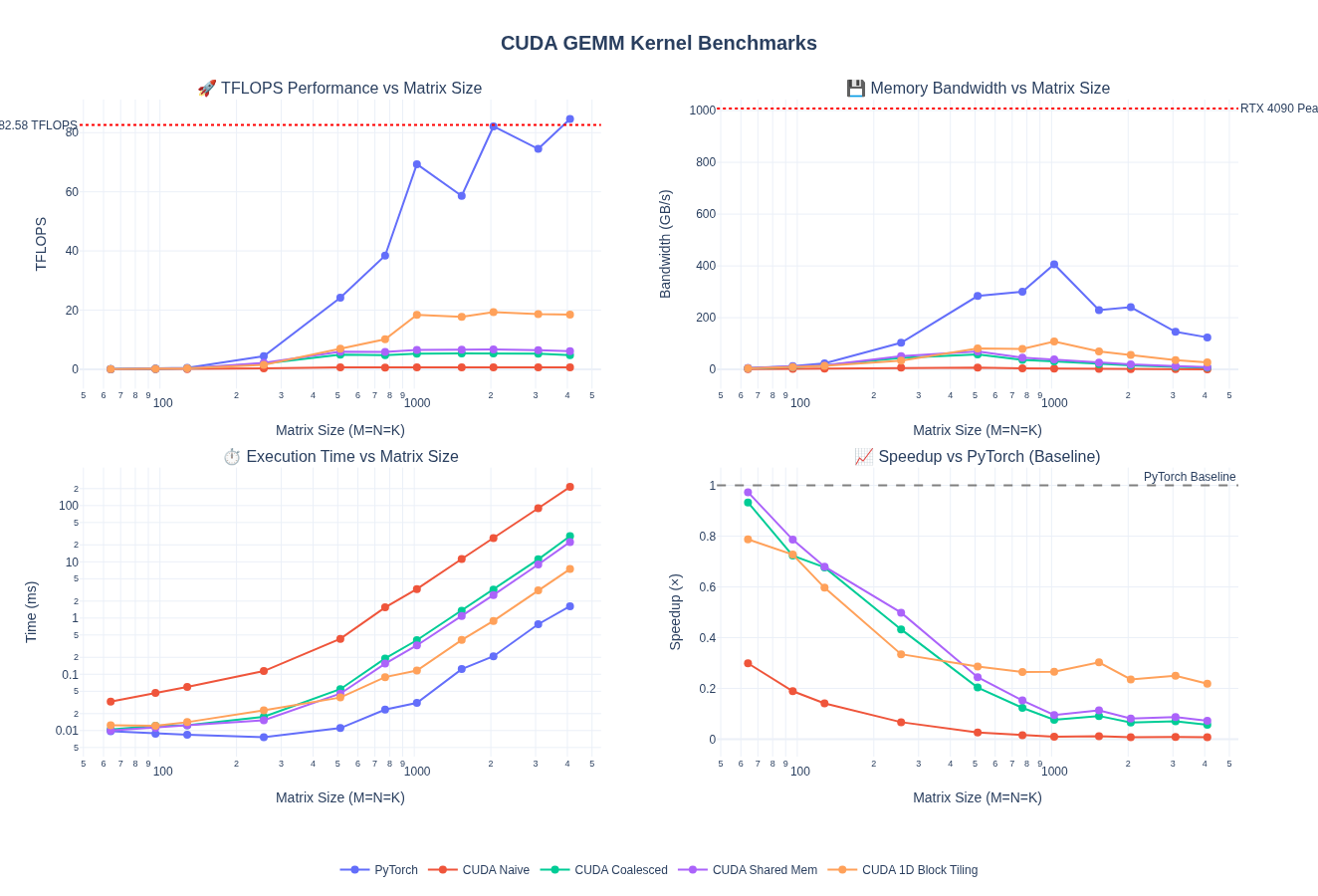
The vectorized kernel shows mixed results — performance degrades compared to 2D block tiling for small to medium matrices but shows significant improvements at larger sizes.

Performance at 4096×4096:

  • 1.27× TFLOPS improvement over 2D block tiling (30.85 → 39.00 TFLOPS)
  • 1.26× bandwidth improvement (45.19 → 57.14 GB/s)
  • 46.3% of PyTorch’s performance (84.23 TFLOPS)
  • 59.7× faster than naive (0.653 → 39.00 TFLOPS)

Performance Across Matrix Sizes

Vectorized performance

Comparison vs Previous Kernels (4096×4096):

KernelTime (ms)TFLOPSBandwidth (GB/s)vs PyTorchSpeedup over Naive
Naive210.330.650.960.8%1.0×
Coalesced26.925.117.486.1%7.8×
Shared Memory22.426.138.987.3%9.4×
1D Block Tiling7.4418.4827.0721.9%28.3×
2D Block Tiling4.4630.8545.1936.6%47.3×
Vectorized3.5239.0057.1446.3%59.7×
PyTorch1.6384.23123.38100%129.0×

Nice! We are at almost 60% for the peak performance for 4096 x 4096! Let’s keep going!

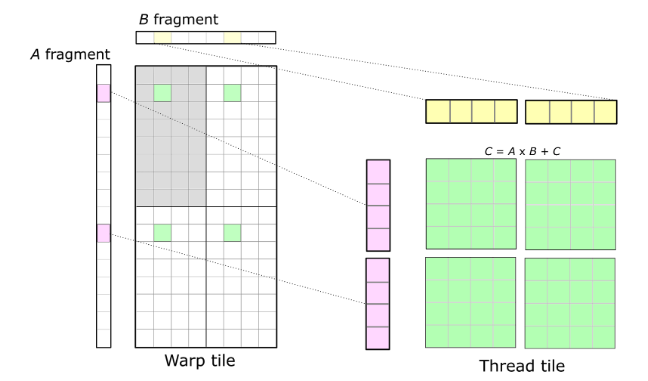
Warp Tiling

Concept

After optimizing thread-level and block-level tiling, the next step is warp-level tiling to exploit the natural 32-thread warp execution unit. This can be leveraged to achieve better register reuse and computation efficiency.

What is Warp Tiling?

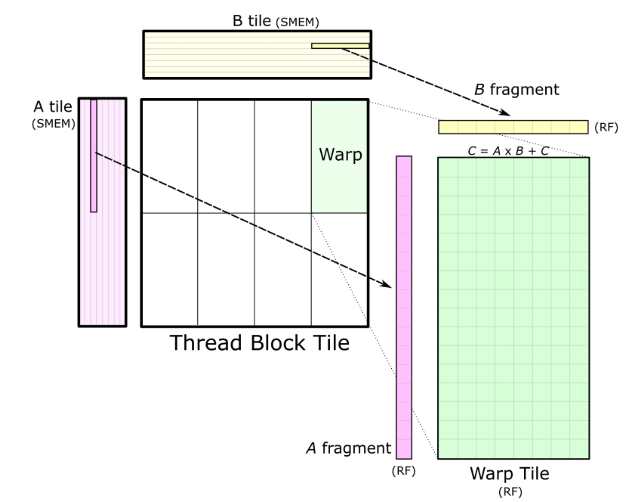
As we have discussed previously, a warp is the fundamental execution unit in NVIDIA GPUs consisting of 32 threads that execute in SIMT (Single Instruction, Multiple Thread) fashion. Warp tiling introduces an additional level in the memory hierarchy.

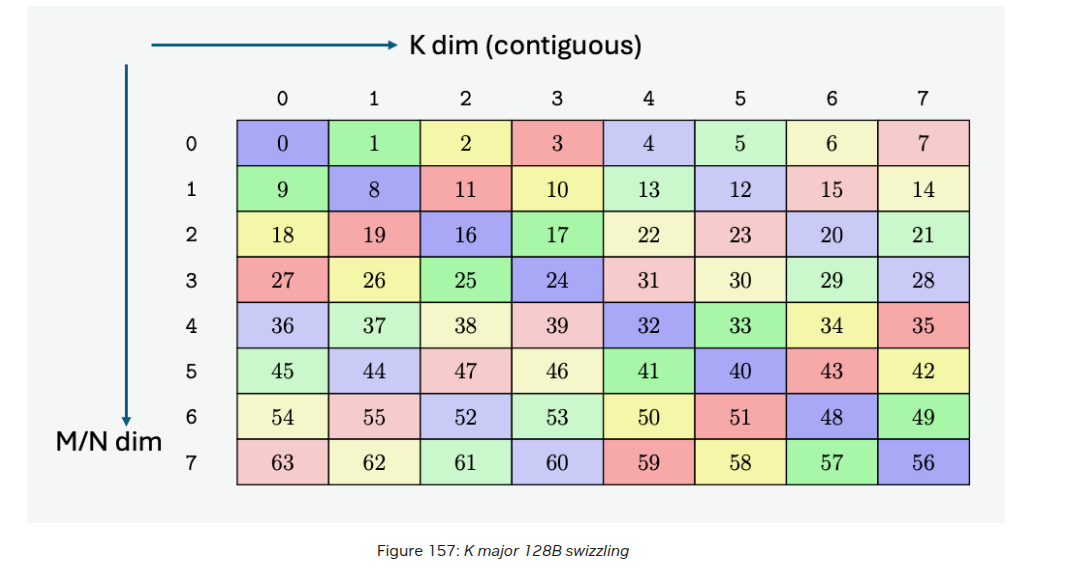
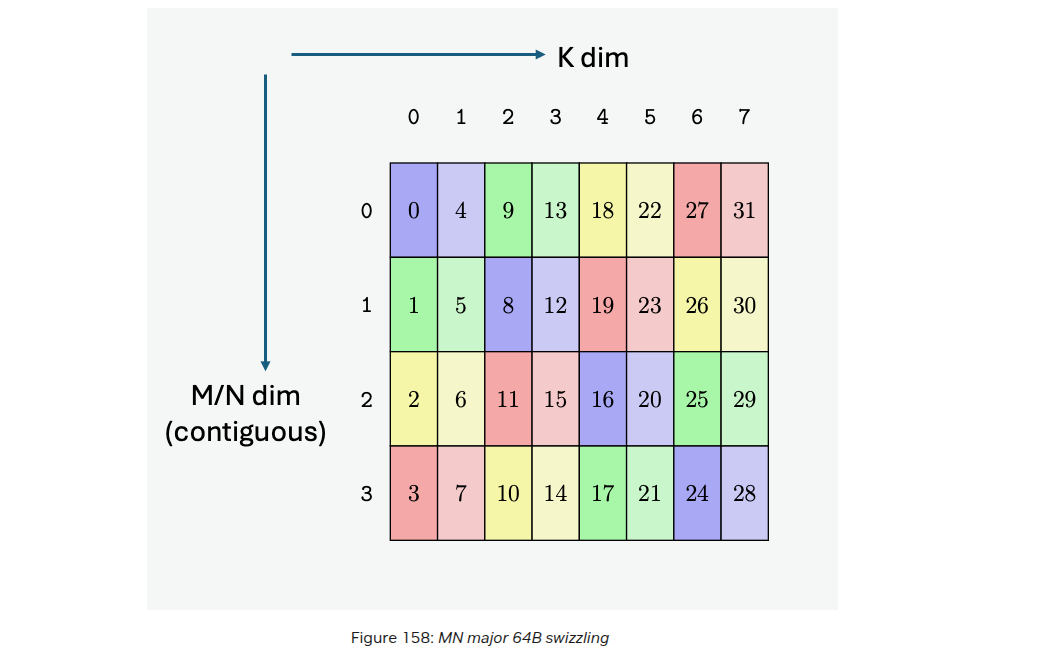
FWIW - we are slowly approaching cutlass territory. Cutlass library implements a sophisticated tiling strategy that mirrors the GPU’s memory hierarchy at multiple levels

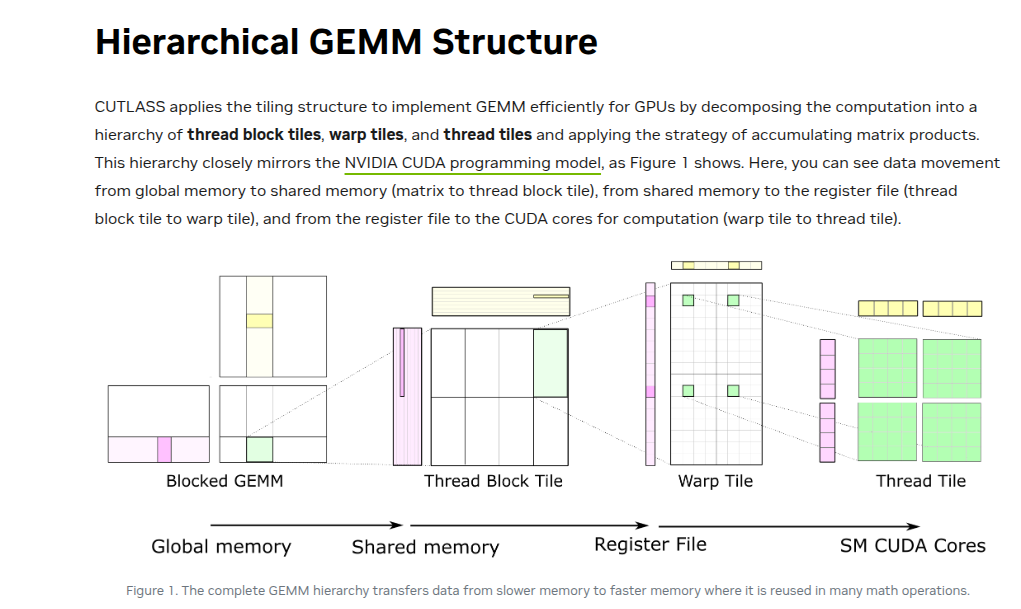CUTLASS Memory Hierarchy Source: NVIDIA CUTLASS Blog

To take advantage of this hierarchy, warps can offer another layer of tiling such that while loading data from shared memory into registers, we do it at warp tile level. In addition, each thread in the warp then calculates its own small fraction of computation.

Nvidia blog warp tiling

Thread tile (next level tiling) is effectively 2D Tiling that we discussed in the previous section.

Nvidia blog thread tiling

Pseudo code for this process looks like:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

for (k = 0; k < K; k += BK) {
    // 1. Load A_tile[BM x BK] and B_tile[BK x BN] into shared memory
    __syncthreads();

    // 2. Each warp loads its own subtile of A and B into registers
    //    (from shared memory)
    for (int kk = 0; kk < BK; ++kk) {
        // 3. Each thread computes on its own 4x4 tile in registers
        C_reg[m][n] += A_frag[m][kk] * B_frag[kk][n];
    }

    __syncthreads();
}

// 4. Write C_reg results from each thread to global C

In the later sections, we will look into Tensor Cores. Enabling warp-tiling is a key milestone for us to get there. But let’s first look at how this works through below visualization with sample values for tile widths and warp size:

NVIDIA CUTLASS Documentation has a lot more details and is pretty comprehensive in explaining different layers of tiling.

Kernel

NOTE: I have removed the non-block size mulitple kernel handling below since the code is getting fairly complicated with multiple layers of nesting for different levels of tiles. I will continue to ignore tail handling in subsequent sections.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170

constexpr int WARPSIZE = 32;

/*
Warp-level tiling GEMM kernel.
Hierarchy: Block (BM x BN) → Warps (WM x WN) → Warp Subtiles (WSUBM x WSUBN) → Thread Tiles (TM x TN)
*/
template <const int BM, const int BN, const int BK, const int row_stride_a, const int row_stride_b>
__device__ void load_from_gmem(int num_cols_b, int num_cols_a,
                               const float *matrix_a, const float *matrix_b,
                               float *tile_a, float *tile_b,
                               int inner_row_a, int inner_col_a,
                               int inner_row_b, int inner_col_b)
{
    for (uint offset = 0; offset + row_stride_a <= BM; offset += row_stride_a)
    {
        const float4 tmp_a = reinterpret_cast<const float4 *>(
            &matrix_a[(inner_row_a + offset) * num_cols_a + inner_col_a * 4])[0];
        tile_a[(inner_col_a * 4 + 0) * BM + inner_row_a + offset] = tmp_a.x;
        tile_a[(inner_col_a * 4 + 1) * BM + inner_row_a + offset] = tmp_a.y;
        tile_a[(inner_col_a * 4 + 2) * BM + inner_row_a + offset] = tmp_a.z;
        tile_a[(inner_col_a * 4 + 3) * BM + inner_row_a + offset] = tmp_a.w;
    }

    for (uint offset = 0; offset + row_stride_b <= BK; offset += row_stride_b)
    {
        reinterpret_cast<float4 *>(
            &tile_b[(inner_row_b + offset) * BN + inner_col_b * 4])[0] =
            reinterpret_cast<const float4 *>(
                &matrix_b[(inner_row_b + offset) * num_cols_b + inner_col_b * 4])[0];
    }
}

template <const int BM, const int BN, const int BK, const int WM, const int WN,
          const int WMITER, const int WNITER, const int WSUBM, const int WSUBN,
          const int TM, const int TN>
__device__ void process_warp_tile(float *register_m, float *register_n, float *thread_results,
                                  const float *tile_a, const float *tile_b,
                                  const uint warp_row, const uint warp_col,
                                  const uint thread_row_in_warp, const uint thread_col_in_warp)
{
    for (uint dot_idx = 0; dot_idx < BK; ++dot_idx)
    {
        for (uint wsub_row_idx = 0; wsub_row_idx < WMITER; ++wsub_row_idx)
        {
            for (uint i = 0; i < TM; ++i)
            {
                register_m[wsub_row_idx * TM + i] =
                    tile_a[(dot_idx * BM) + warp_row * WM + wsub_row_idx * WSUBM +
                           thread_row_in_warp * TM + i];
            }
        }

        for (uint wsub_col_idx = 0; wsub_col_idx < WNITER; ++wsub_col_idx)
        {
            for (uint i = 0; i < TN; ++i)
            {
                register_n[wsub_col_idx * TN + i] =
                    tile_b[(dot_idx * BN) + warp_col * WN + wsub_col_idx * WSUBN +
                           thread_col_in_warp * TN + i];
            }
        }

        for (uint wsub_row_idx = 0; wsub_row_idx < WMITER; ++wsub_row_idx)
        {
            for (uint wsub_col_idx = 0; wsub_col_idx < WNITER; ++wsub_col_idx)
            {
                for (uint res_idx_m = 0; res_idx_m < TM; ++res_idx_m)
                {
                    for (uint res_idx_n = 0; res_idx_n < TN; ++res_idx_n)
                    {
                        thread_results[(wsub_row_idx * TM + res_idx_m) * (WNITER * TN) +
                                       (wsub_col_idx * TN) + res_idx_n] +=
                            register_m[wsub_row_idx * TM + res_idx_m] *
                            register_n[wsub_col_idx * TN + res_idx_n];
                    }
                }
            }
        }
    }
}

template <const int BM, const int BN, const int BK, const int WM, const int WN,
          const int WNITER, const int TM, const int TN, const int NUM_THREADS>
__global__ void __launch_bounds__(NUM_THREADS)
    sgemm_warptiling_kernel(int num_rows_a, int num_cols_b, int num_cols_a,
                            float alpha, const float *matrix_a, const float *matrix_b,
                            float beta, float *matrix_c)
{
    const uint block_row = blockIdx.y;
    const uint block_col = blockIdx.x;

    const uint warp_idx = threadIdx.x / WARPSIZE;
    const uint warp_col = warp_idx % (BN / WN);
    const uint warp_row = warp_idx / (BN / WN);

    constexpr uint WMITER = (WM * WN) / (WARPSIZE * TM * TN * WNITER);
    constexpr uint WSUBM = WM / WMITER;
    constexpr uint WSUBN = WN / WNITER;

    const uint thread_idx_in_warp = threadIdx.x % WARPSIZE;
    const uint thread_col_in_warp = thread_idx_in_warp % (WSUBN / TN);
    const uint thread_row_in_warp = thread_idx_in_warp / (WSUBN / TN);

    __shared__ float tile_a[BM * BK];
    __shared__ float tile_b[BK * BN];

    matrix_a += block_row * BM * num_cols_a;
    matrix_b += block_col * BN;
    matrix_c += (block_row * BM + warp_row * WM) * num_cols_b + block_col * BN + warp_col * WN;

    const uint inner_row_a = threadIdx.x / (BK / 4);
    const uint inner_col_a = threadIdx.x % (BK / 4);
    constexpr uint row_stride_a = (NUM_THREADS * 4) / BK;

    const uint inner_row_b = threadIdx.x / (BN / 4);
    const uint inner_col_b = threadIdx.x % (BN / 4);
    constexpr uint row_stride_b = NUM_THREADS / (BN / 4);

    float thread_results[WMITER * TM * WNITER * TN] = {0.0f};
    float register_m[WMITER * TM] = {0.0f};
    float register_n[WNITER * TN] = {0.0f};

    for (uint block_k_idx = 0; block_k_idx < num_cols_a; block_k_idx += BK)
    {
        load_from_gmem<BM, BN, BK, row_stride_a, row_stride_b>(
            num_cols_b, num_cols_a, matrix_a, matrix_b, tile_a, tile_b,
            inner_row_a, inner_col_a, inner_row_b, inner_col_b);

        __syncthreads();

        process_warp_tile<BM, BN, BK, WM, WN, WMITER, WNITER, WSUBM, WSUBN, TM, TN>(
            register_m, register_n, thread_results, tile_a, tile_b,
            warp_row, warp_col, thread_row_in_warp, thread_col_in_warp);

        matrix_a += BK;
        matrix_b += BK * num_cols_b;

        __syncthreads();
    }

    for (uint wsub_row_idx = 0; wsub_row_idx < WMITER; ++wsub_row_idx)
    {
        for (uint wsub_col_idx = 0; wsub_col_idx < WNITER; ++wsub_col_idx)
        {
            float *matrix_c_interim = matrix_c + (wsub_row_idx * WSUBM) * num_cols_b +
                                      wsub_col_idx * WSUBN;

            for (uint res_idx_m = 0; res_idx_m < TM; res_idx_m += 1)
            {
                for (uint res_idx_n = 0; res_idx_n < TN; res_idx_n += 4)
                {
                    float4 tmp_c = reinterpret_cast<float4 *>(
                        &matrix_c_interim[(thread_row_in_warp * TM + res_idx_m) * num_cols_b +
                                          thread_col_in_warp * TN + res_idx_n])[0];

                    const int res_idx = (wsub_row_idx * TM + res_idx_m) * (WNITER * TN) +
                                        wsub_col_idx * TN + res_idx_n;
                    tmp_c.x = alpha * thread_results[res_idx + 0] + beta * tmp_c.x;
                    tmp_c.y = alpha * thread_results[res_idx + 1] + beta * tmp_c.y;
                    tmp_c.z = alpha * thread_results[res_idx + 2] + beta * tmp_c.z;
                    tmp_c.w = alpha * thread_results[res_idx + 3] + beta * tmp_c.w;

                    reinterpret_cast<float4 *>(
                        &matrix_c_interim[(thread_row_in_warp * TM + res_idx_m) * num_cols_b +
                                          thread_col_in_warp * TN + res_idx_n])[0] = tmp_c;
                }
            }
        }
    }
}

__launch_bounds__ trick was something I learnt after reading a few kernels. It allows us to control kernel occupancy by setting a limit on per-thread register usage i.e by specifying the thread block size and the target number of blocks per SM, the compiler adjusts register allocation accordingly. This was a good resource to understand this attribute.

Caller

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

template <const int BM, const int BN, const int BK, const int WM, const int WN,
          const int WNITER, const int TM, const int TN, const int NUM_THREADS>
void sgemm_warptiling(const torch::Tensor &matrix_a, const torch::Tensor &matrix_b,
                      torch::Tensor &output_matrix, float alpha, float beta)
{
    // .. similar to previous kernels
    constexpr int WMITER = (WM * WN) / (WARPSIZE * TM * TN * WNITER);
    constexpr int WSUBM = WM / WMITER;
    constexpr int WSUBN = WN / WNITER;
    static_assert(WMITER * WSUBM == WM, "WMITER * WSUBM must equal WM");
    static_assert(WNITER * WSUBN == WN, "WNITER * WSUBN must equal WN");
    static_assert((BM % WM == 0) && (BN % WN == 0), "Block tile must be divisible by warp tile");
    static_assert((WSUBM % TM == 0) && (WSUBN % TN == 0), "Warp subtile must be divisible by thread tile");

    // Configure kernel launch
    dim3 block_dim(NUM_THREADS);
    dim3 grid_dim(CEIL_DIV(num_cols_b, BN), CEIL_DIV(num_rows_a, BM));

    // Launch kernel
    sgemm_warptiling_kernel<BM, BN, BK, WM, WN, WNITER, TM, TN, NUM_THREADS>
        <<<grid_dim, block_dim>>>(
            num_rows_a, num_cols_b, num_cols_a,
            alpha, d_matrix_a, d_matrix_b, beta, d_output_matrix);
}

// Default configuration wrapper
void sgemm_warptiling_default(const torch::Tensor &matrix_a, const torch::Tensor &matrix_b,
                               torch::Tensor &output_matrix, float alpha, float beta)
{
    // Default configuration: BM=128, BN=128, BK=16, WM=64, WN=64, WNITER=4, TM=8, TN=4, NUM_THREADS=128
    // This gives: WMITER=2, WSUBM=32, WSUBN=16
    // Warps per block: (128*128)/(64*64) = 4 warps
    // Threads needed: 4 warps * 32 threads/warp = 128 threads
    sgemm_warptiling<128, 128, 16, 64, 64, 4, 8, 4, 128>(
        matrix_a, matrix_b, output_matrix, alpha, beta);
}

Performance Analysis

The warp tiling kernel shows further performance gains at large matrix sizes, achieving the best performance so far.

Performance at 4096×4096:

  • 1.17× TFLOPS improvement over vectorized kernel (39.07 → 45.82 TFLOPS)
  • 1.17× bandwidth improvement (57.24 → 67.12 GB/s)
  • 54.4% of PyTorch’s performance (84.19 TFLOPS)
  • 70.1× faster than naive (0.654 → 45.82 TFLOPS)

Comparison vs Previous Kernels (4096×4096):

KernelTime (ms)TFLOPSBandwidth (GB/s)vs PyTorchSpeedup over Naive
Naive210.290.650.960.8%1.0×
Coalesced26.955.107.476.1%7.8×
Shared Memory22.406.148.997.3%9.4×
1D Block Tiling7.4218.5227.1322.0%28.3×
2D Block Tiling4.4530.8945.2536.7%47.2×
Vectorized3.5239.0757.2446.4%59.8×
Warp Tiling3.0045.8267.1254.4%70.1×
PyTorch1.6384.19123.33100%128.8×

Performance Across Matrix Sizes

Matrix SizeTime (ms)TFLOPSvs PyTorchSpeedup vs 2D Tiling
128×1280.0210.2040.2%0.81×
512×5120.0584.6018.9%0.79×
1024×10240.10320.7729.8%0.90×
2048×20480.39643.3852.6%1.14×
4096×40963.0045.8254.4%1.17×
8192×819225.6942.8050.9%1.12×

Across matrices warptiling

Supporting 16-bit GEMM

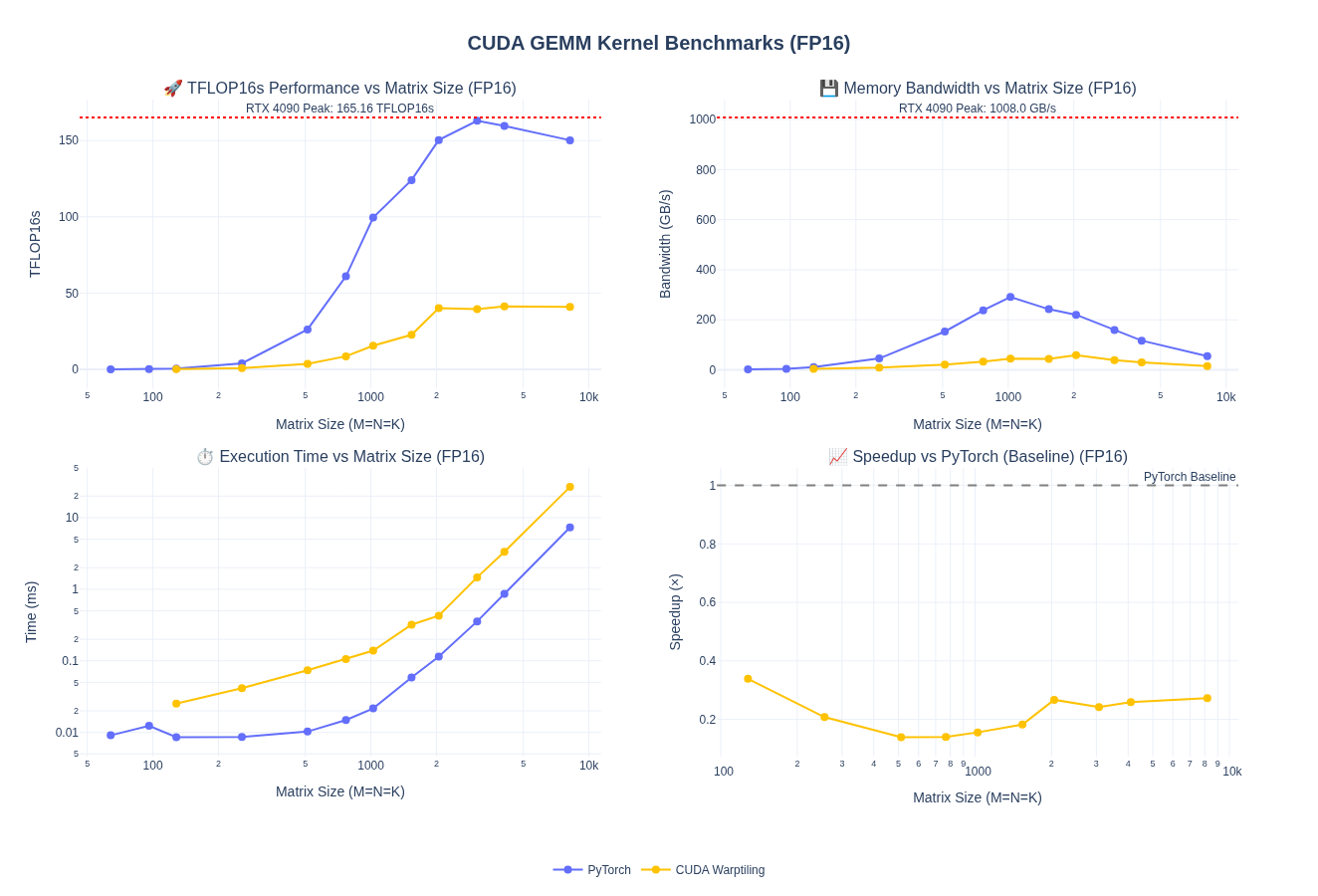
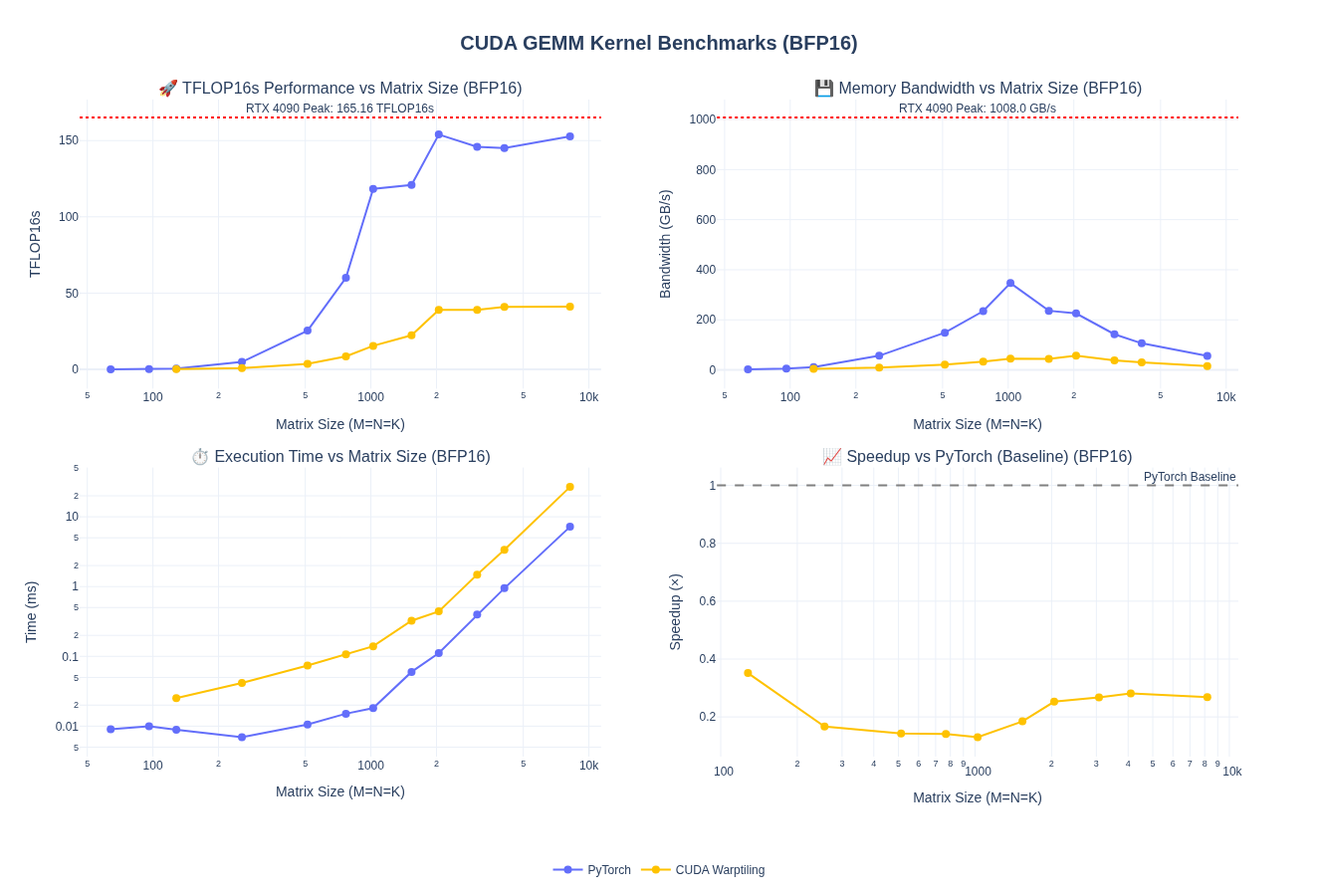
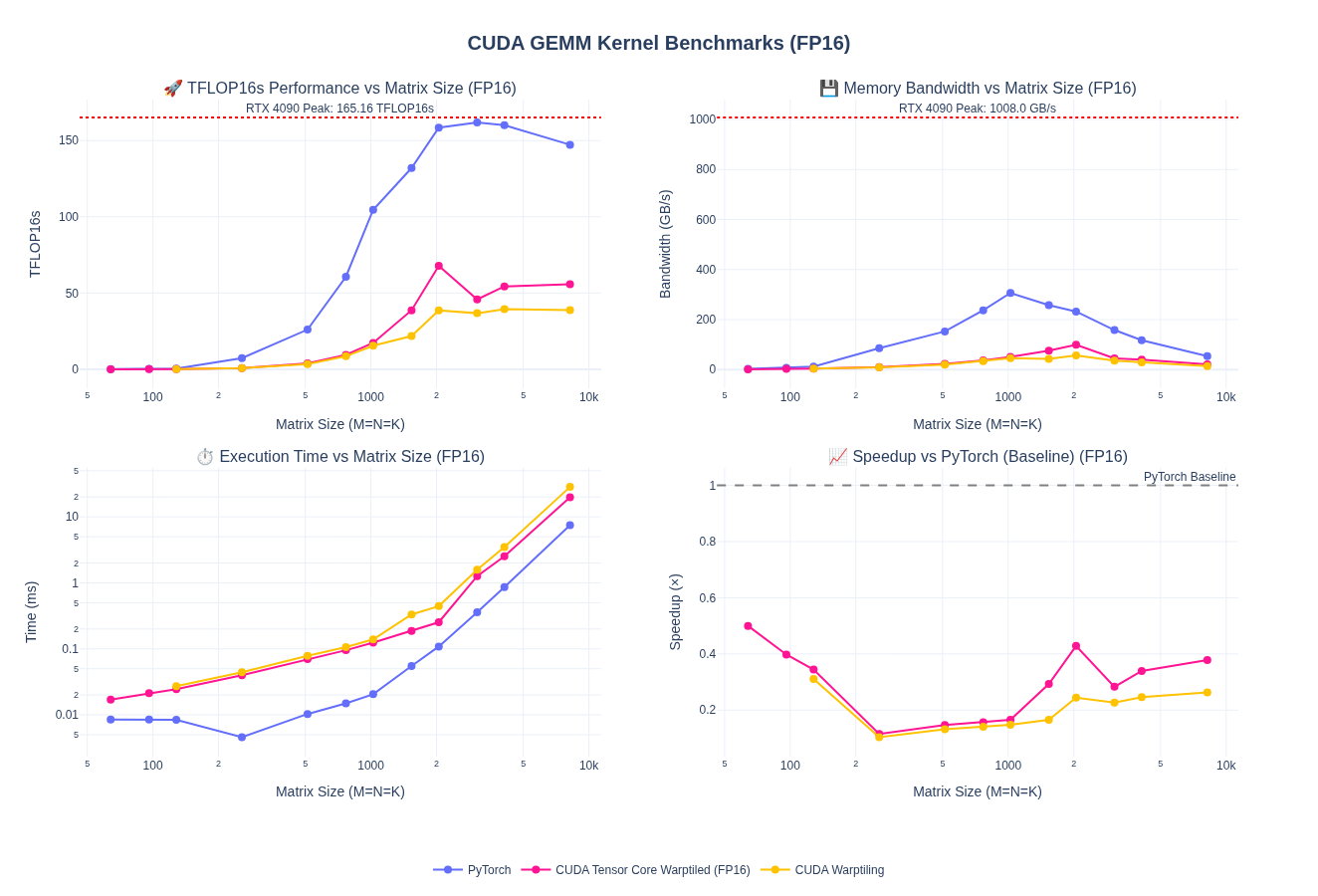
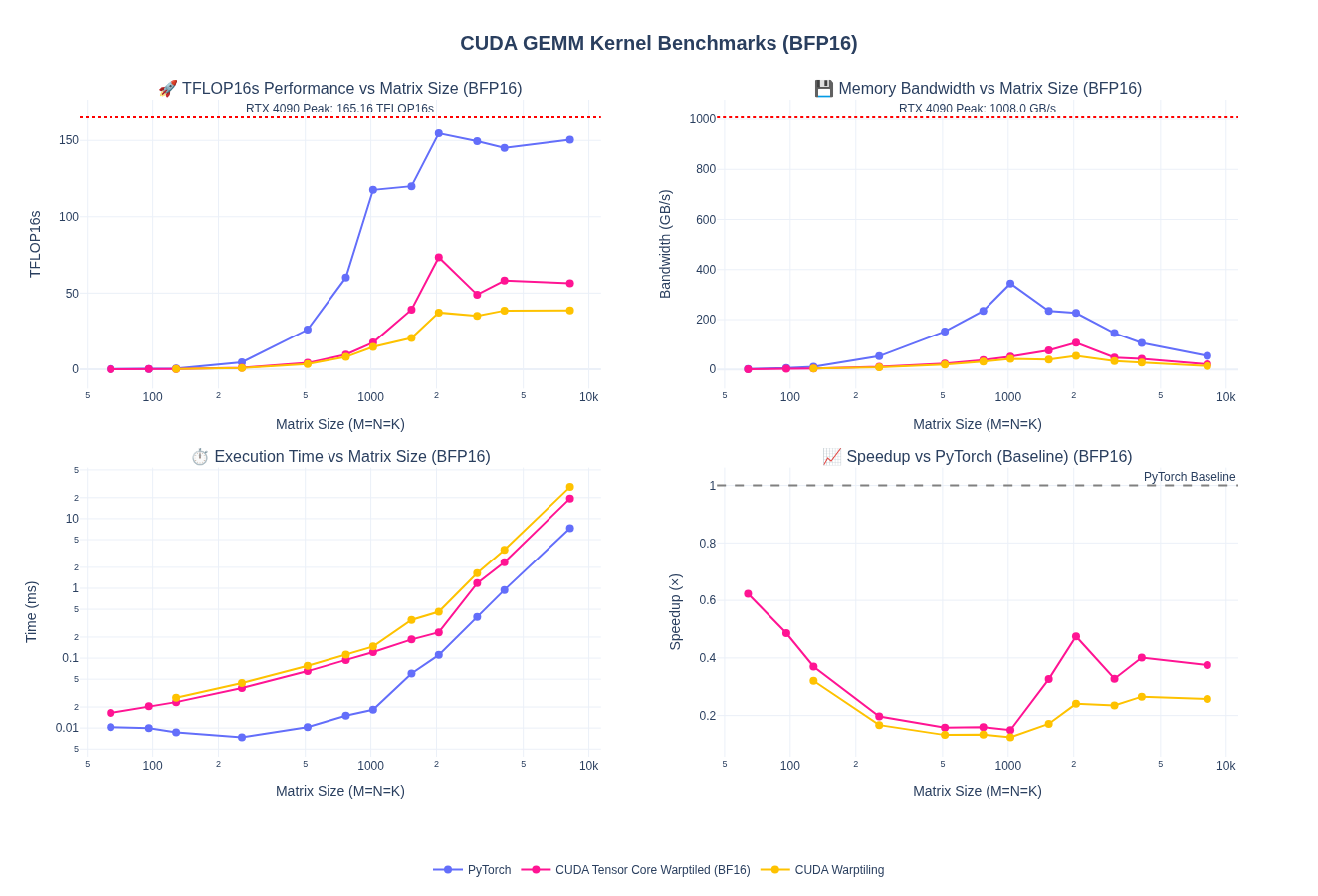
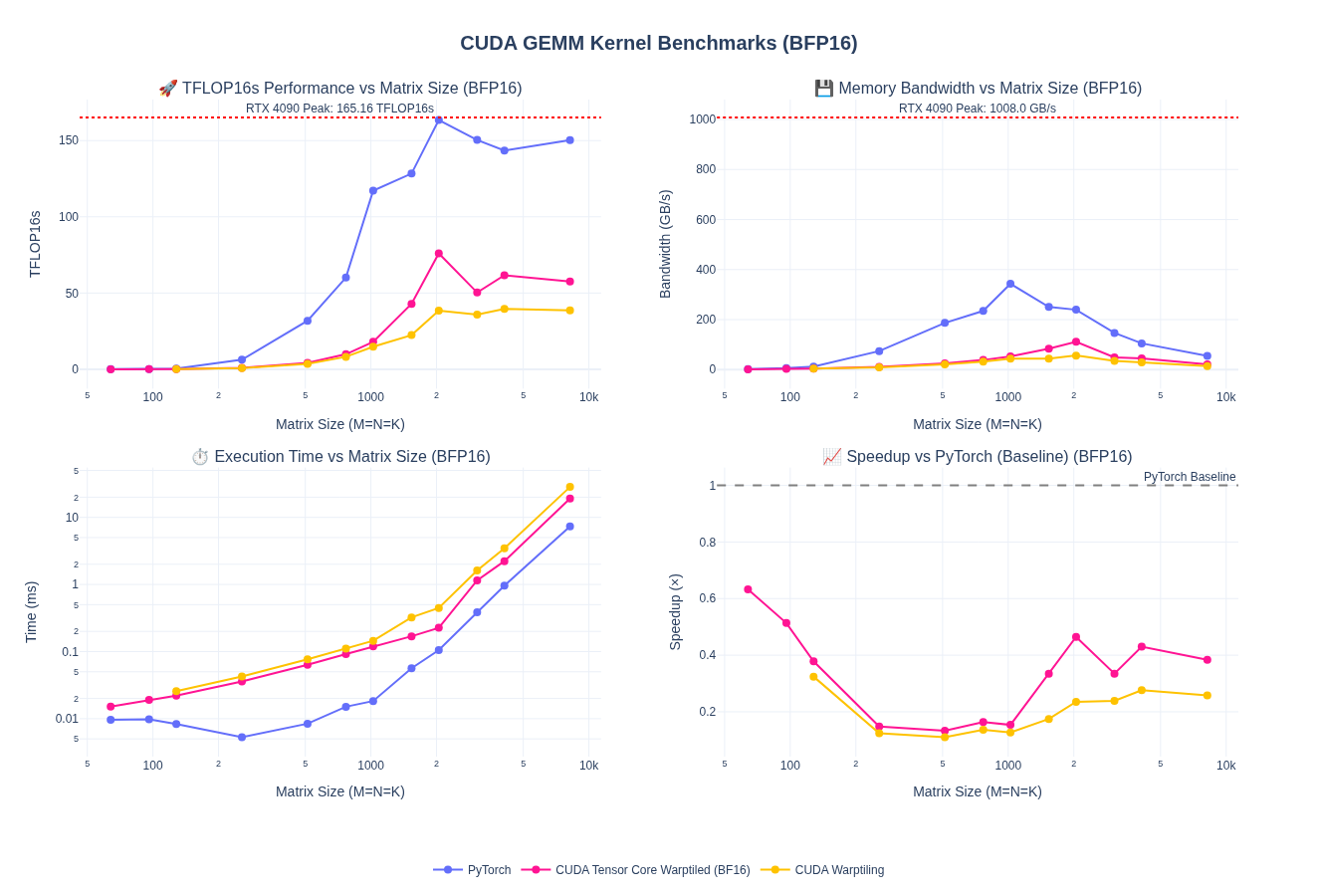
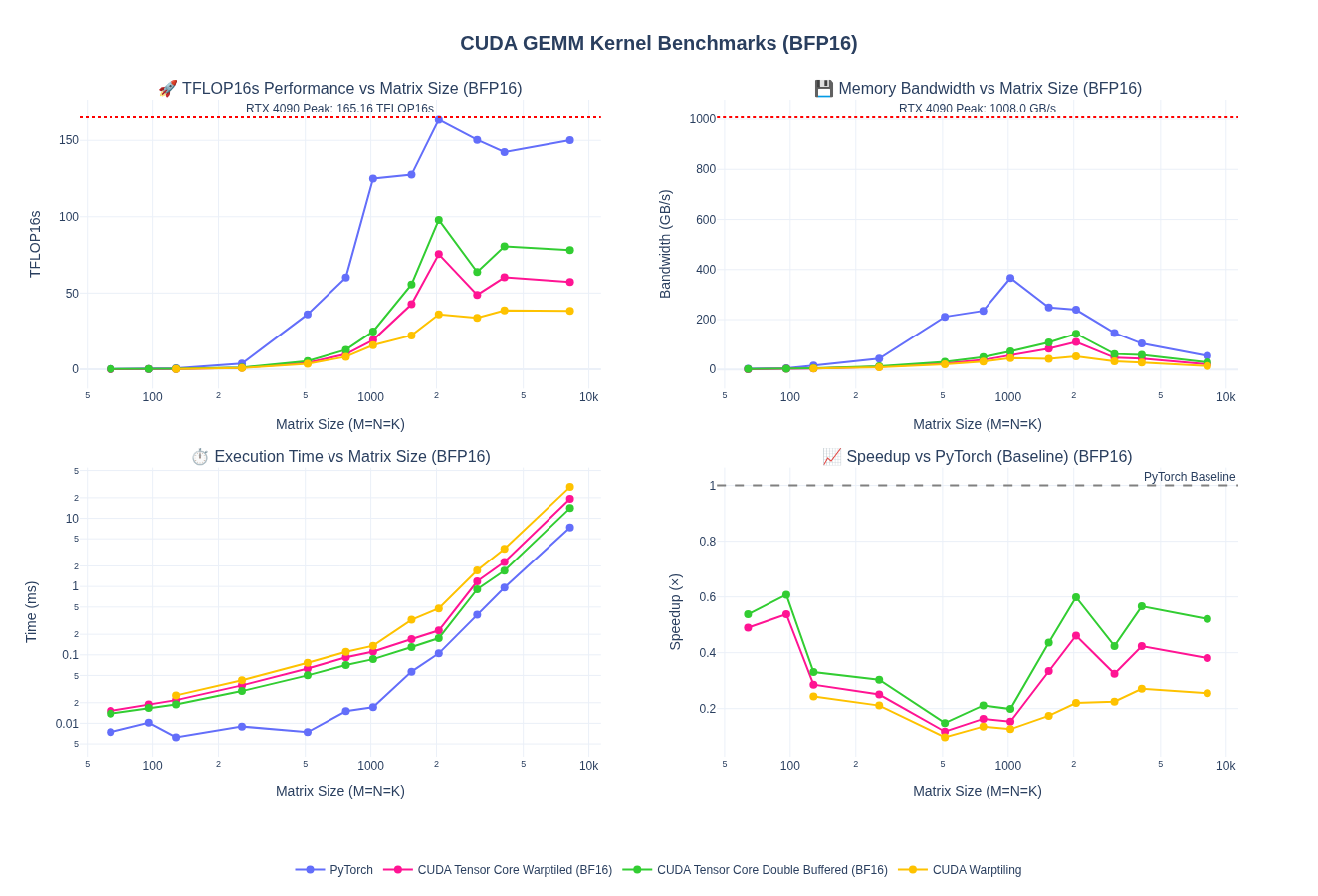
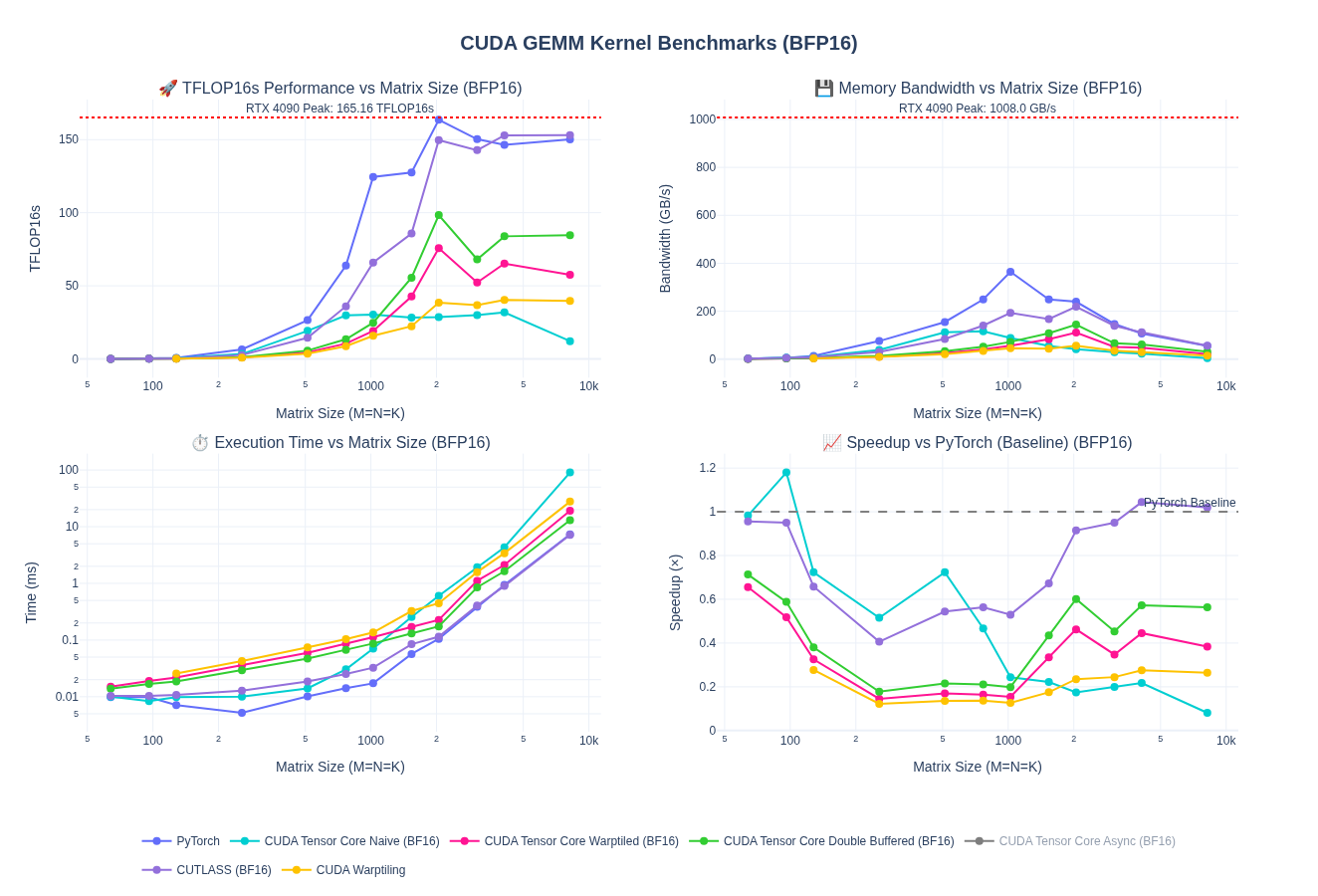
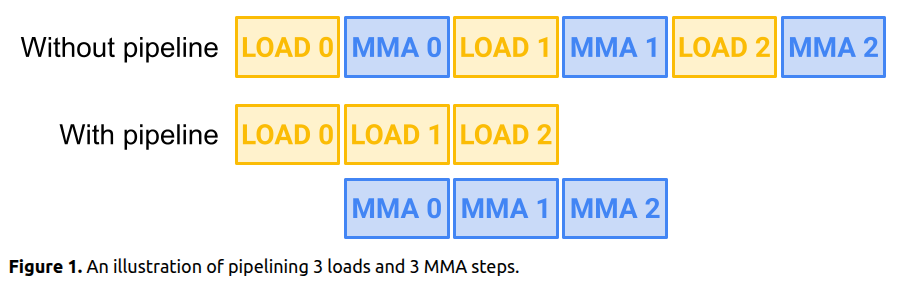
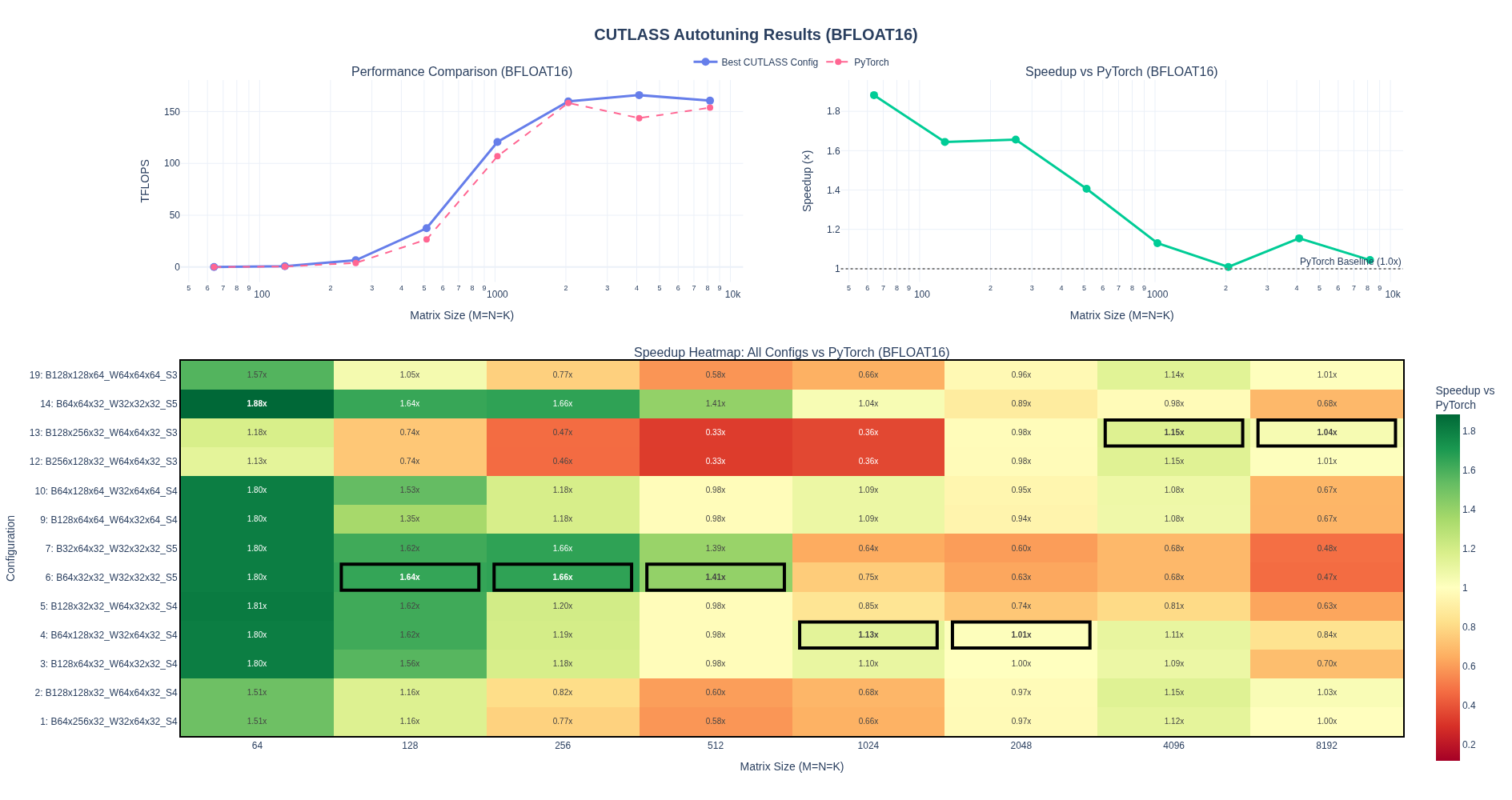
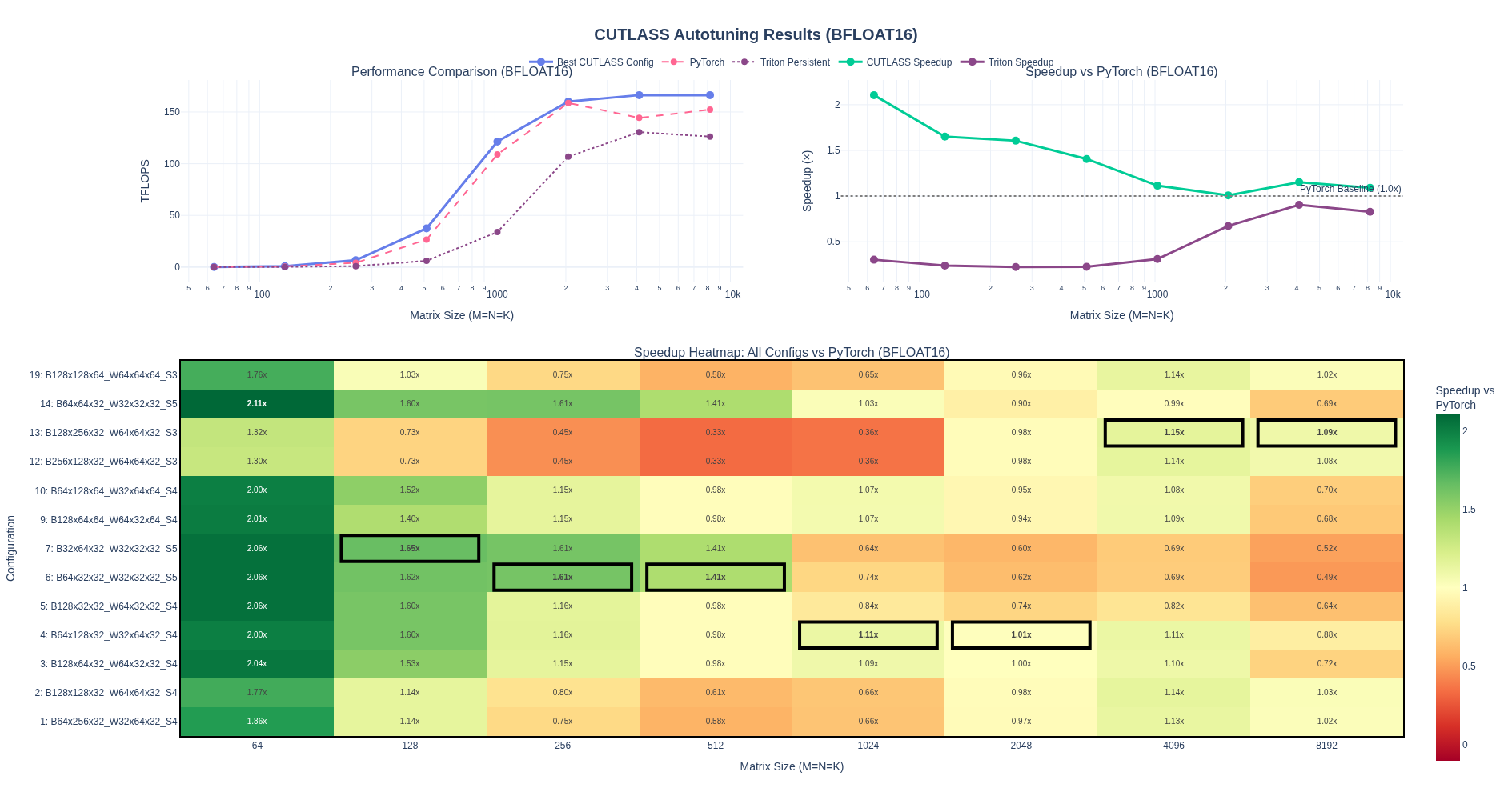
So far, we have worked only on fp32 kernels. Most workloads today increasingly use 16-bit floating-point formats (FP16 and BF16) and even lower precisions such as fp8, fp4, etc to reduce memory bandwidth requirements and increase throughput. While our warp tiling kernel works for FP32, we can extend it to support lower-precision computations in 16-bit. This mostly requires us adapt the kernel to handle multiple dtypes, which is just templating. Although, one thing to note is to get good numeric behavior on the lower prevision kernels, we need to ensure we do accumulation in higher precision such as fp32.

I am leaving out the kernel implementation for this part so we can focus on WMMA and Tensor Cores next. However, here is the baseline performance after porting warptiling technique for fp32 above to fp16/bf16. Spoiler alert: the performance is pretty bad and we are down to about 1/4th of pytorch performance.

NOTE: I haven’t done any tuning of the tile sizes here - just took fp32 kernel as is and update types and handled vectorized loads using float2.

FP16 Baseline

BFP16 Baseline

Quick Takeaway: without tensorcores we can’t match the performance of pytorch. So, let’s look at that next!!

WMMA and Tensorcores

The warp-tiling structure that we discussed earlier can also be implemented using nvidia WMMA api (Warp Matrix Multiply-Accumulate). WMMA provides extensions to the tiling structure and exposes Tensorcore MMA operations.

NOTE: CUTLASS provide even more high-level abstractions for GEMMs. We will discuss that later

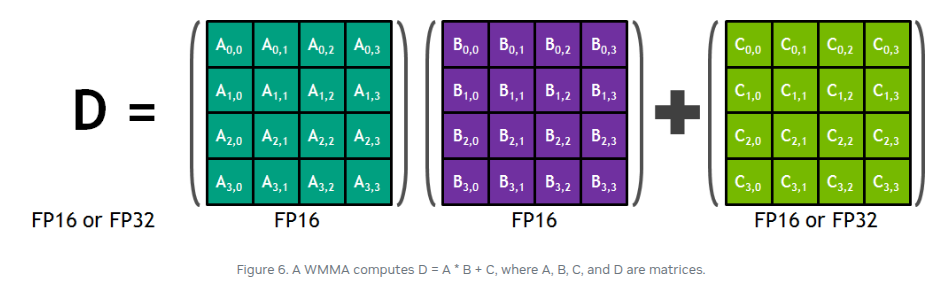
Before we dig further into WMMA, let’s look at what are Tensorcores. At a high level, Tensorcores provide warp-level collective operation for MMA such that 32 threads within a warp collectively hold MMA operands. In other words, the thread-tiling register based outer product can be lowered all the way to the hardware using Tensorcores. Below we represent 4 x 4 x 4 matrix processing array performing D = A * B + C.

WMMA

Digging a little into specific, here is a good common use case for fp16 matmul with fp32 accumulation:

Tensorcore example

can be codified as

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

float D[4];
uint32_t const A[2];
uint32_t const B;
float const C[4];
// Example targets 16-by-8-by-8 Tensor Core operation
asm(
    "mma.sync.aligned.m16n8k8.row.col.f32.f16.f16.f32 "
    " { %0, %1, %2, %3 }, "
    " { %4, %5}, "
    " %6, "
    " { %7, %8, %9, %10 };"
    :
    "=f"(D[0]), "=f"(D[1]), "=f"(D[2]), "=f"(D[3])
    :
    "r"(A[0]), "r"(A[1]),
    "r"(B),
    "f"(C[0]), "f"(C[1])
);

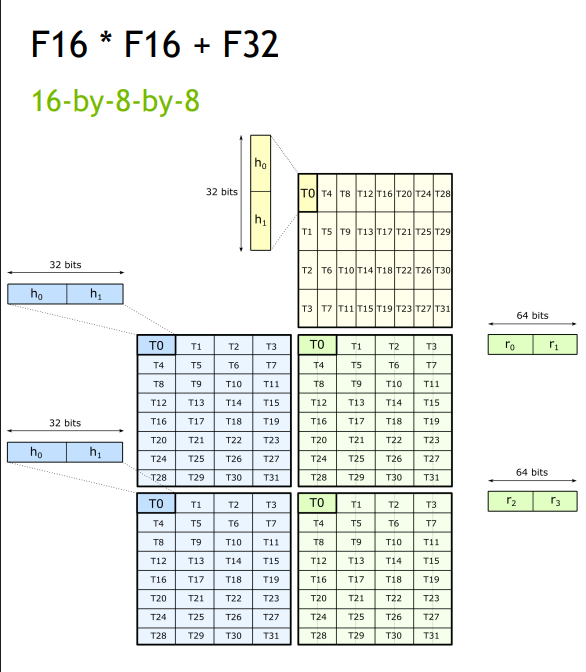
Here, mma.sync.aligned.m16n8k8.row.col.f32.f16.f16.f32 can be understood as mma.sync.aligned instruction over matrix dimentsion of M=16, N=8, K=8 (computes C[16×8] = A[16×8] × B[8×8] + C[16×8]). row.col represents row-major/column-major layouts for A and B, respectivelly and finally f32.f16.f16.f32 represents data types such that output is 32-bit float (fp32) with A and B as fp16 and accumulation happening in fp32.

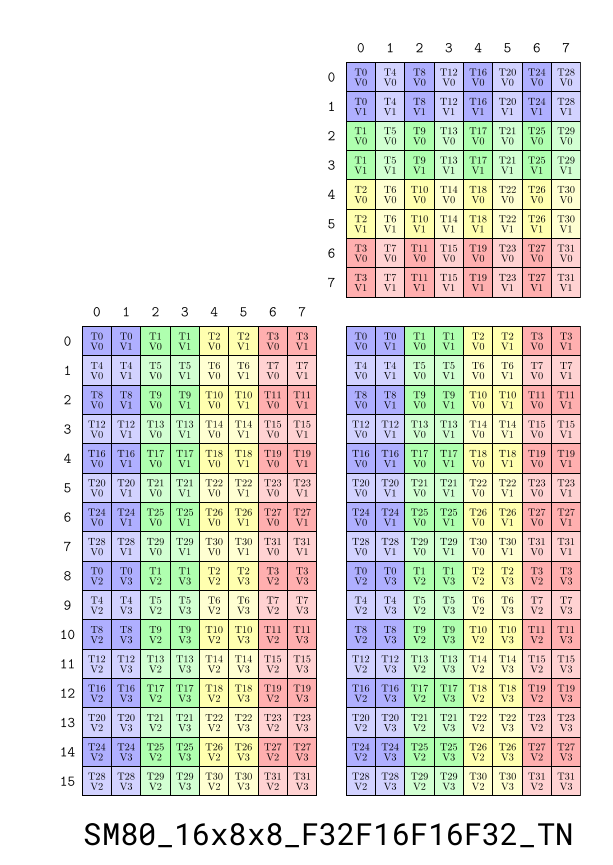
SM80 TC Instruction

Below is the Tensorcore operation on my RTX 4090 for Ada.

SM80 TC Instruction

More details on Tensorcore instructions in this GTC talk from 2019.

WMMA GEMM Kernel

So, as we see above, the general idea is that NVidia provides instruction sets for Tensor Cores to do warp level matmuls that allow us to calculate thread tile matrix multiplications in single instructions. These instructions allow warp-wide MMA operations. Quoted from original Cutlass post:

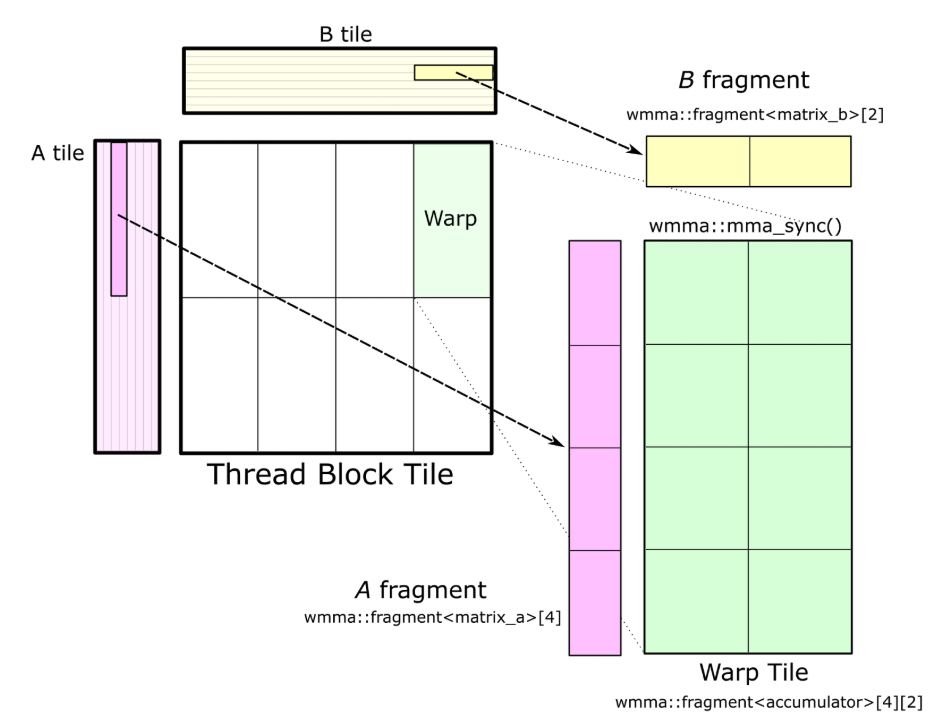
Figure shows the warp tile structure that targets the CUDA WMMA API. Calls to wmma::load_matrix_sync load fragments of A and B into instances of the nvcuda::wmma::fragment<> template, and the accumulator elements for the warp tile are structured as an array of nvcuda::wmma::fragment<accumulator> objects. These fragments store a 2D matrix distributed among the threads of the warp. Finally, calls to nvcuda::wmma::mma_sync() for each accumulator fragment (and corresponding fragments from A and B) compute the warp-wide matrix multiply-accumulate operation using Tensor Cores.

Source: CUTLASS: Fast Linear Algebra in CUDA C++

WMMA 2

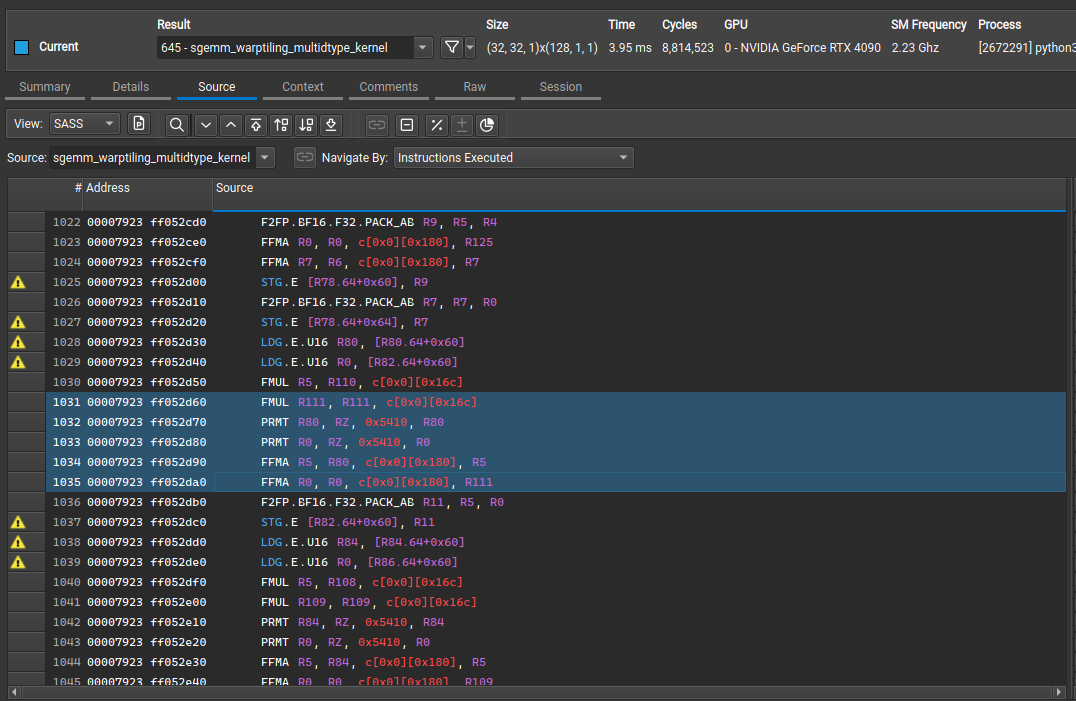
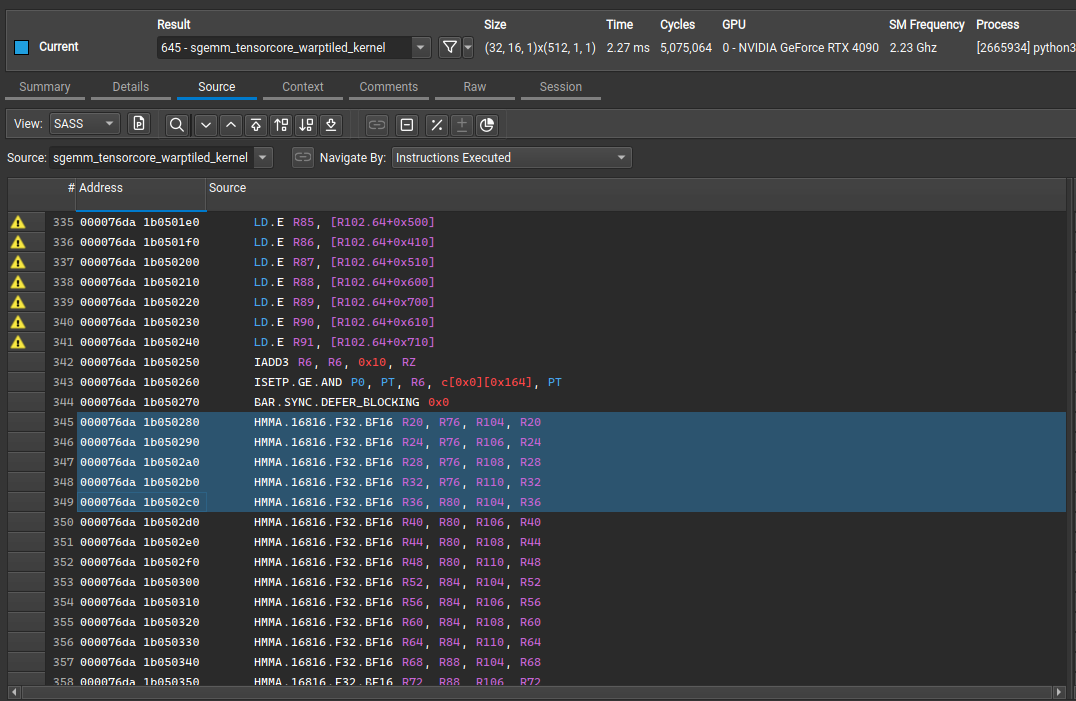
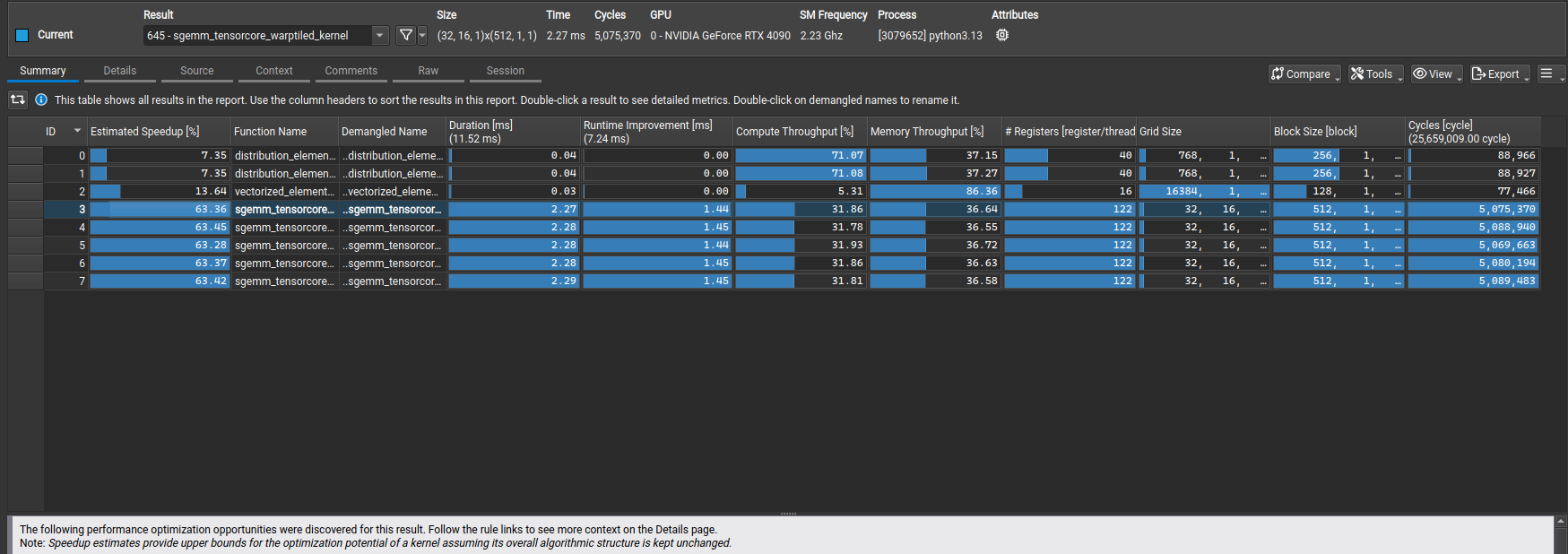
Now, using reference naive tensorcore kernel using wmma, the baseline performance was pretty bad. So next, let’s transform our original warp-tiled kernel for 16-bit precision to wmma api. We should be able to map tile sizes directly to wmma api.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128

template <typename InputType,
            const int BLOCK_ROW_WARPS = 4,
            const int BLOCK_COL_WARPS = 4,
            const int WARP_ROW_TILES = 4,
            const int WARP_COL_TILES = 2,
            const int WMMA_M = 16,
            const int WMMA_N = 16,
            const int WMMA_K = 16>
__global__ void
sgemm_tensorcore_warptiled_kernel(int num_cols_b, int num_cols_a,
                                    float alpha, const InputType *matrix_a,
                                    const InputType *matrix_b, float beta,
                                    float *matrix_c)
{
    const uint warp_id = threadIdx.x / 32;
    const uint warp_row = warp_id / BLOCK_COL_WARPS;
    const uint warp_col = warp_id % BLOCK_COL_WARPS;

    constexpr int BLOCK_ROW_TILES = WARP_ROW_TILES * BLOCK_ROW_WARPS;
    constexpr int BLOCK_COL_TILES = WARP_COL_TILES * BLOCK_COL_WARPS;

    constexpr int BM = BLOCK_ROW_TILES * WMMA_M;
    constexpr int BN = BLOCK_COL_TILES * WMMA_N;
    constexpr int BK = WMMA_K;

    // Shared memory: tile_a (BM x BK, row-major), tile_b (BK x BN, column-major)
    __shared__ InputType tile_a[BM * BK];
    __shared__ InputType tile_b[BK * BN];

    const InputType *global_a = matrix_a;
    const InputType *global_b = matrix_b;
    float *global_c = matrix_c;

    nvcuda::wmma::fragment<nvcuda::wmma::matrix_a, WMMA_M, WMMA_N, WMMA_K, InputType, nvcuda::wmma::row_major> a_frag;
    nvcuda::wmma::fragment<nvcuda::wmma::matrix_b, WMMA_M, WMMA_N, WMMA_K, InputType, nvcuda::wmma::col_major> b_frag;

    // Accumulator fragments (FP32): each warp maintains WARP_ROW_TILES x WARP_COL_TILES tiles
    nvcuda::wmma::fragment<nvcuda::wmma::accumulator, WMMA_M, WMMA_N, WMMA_K, float> acc_frag[WARP_ROW_TILES][WARP_COL_TILES];
    nvcuda::wmma::fragment<nvcuda::wmma::accumulator, WMMA_M, WMMA_N, WMMA_K, float> c_frag;
#pragma unroll
    for (int i = 0; i < WARP_ROW_TILES; ++i)
    {
#pragma unroll
        for (int j = 0; j < WARP_COL_TILES; ++j)
        {
            nvcuda::wmma::fill_fragment(acc_frag[i][j], 0.0f);
        }
    }

    constexpr int NUM_THREADS = BLOCK_ROW_WARPS * BLOCK_COL_WARPS * 32; // warps per block * threads per warp

    // K-loop: iterate by BK, load A and B tiles, compute WMMA operations
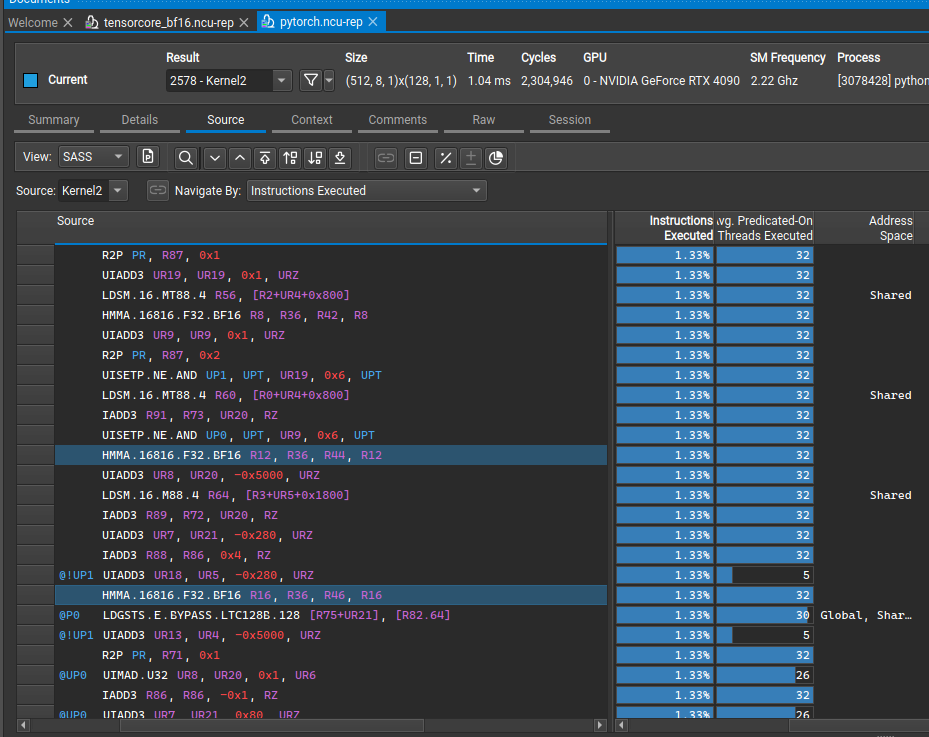
    for (int block_k_idx = 0; block_k_idx < num_cols_a; block_k_idx += BK)
    {
        // Load A tile (BM x BK, row-major)
        // TODO: Vectorize loads if possible - getting numerics issues
        for (int idx = threadIdx.x; idx < BM * BK; idx += NUM_THREADS)
        {
            int row = idx / BK;
            int col = idx % BK;
            int global_row = blockIdx.y * BM + row;
            int global_col = block_k_idx + col;
            tile_a[row * BK + col] = global_a[global_row * num_cols_a + global_col];
        }

        // Load B tile (BK x BN, column-major for WMMA)
        // TODO: Vectorize loads if possible - getting numerics issues
        for (int idx = threadIdx.x; idx < BK * BN; idx += NUM_THREADS)
        {
            int row = idx / BN;
            int col = idx % BN;
            int global_row = block_k_idx + row;
            int global_col = blockIdx.x * BN + col;
            tile_b[col * BK + row] = global_b[global_row * num_cols_b + global_col];
        }

        __syncthreads();

        // Warp-level tiling: each warp computes WARP_ROW_TILES x WARP_COL_TILES WMMA tiles
#pragma unroll
        for (int i = 0; i < WARP_ROW_TILES; ++i)
        {
#pragma unroll
            for (int j = 0; j < WARP_COL_TILES; ++j)
            {
                int a_tile_row = warp_row * WARP_ROW_TILES + i;
                int b_tile_col = warp_col * WARP_COL_TILES + j;

                InputType const *a_tile_ptr = tile_a + (a_tile_row * WMMA_M) * BK;
                InputType const *b_tile_ptr = tile_b + (b_tile_col * WMMA_N) * BK;

                nvcuda::wmma::load_matrix_sync(a_frag, a_tile_ptr, BK);
                nvcuda::wmma::load_matrix_sync(b_frag, b_tile_ptr, BK);
                nvcuda::wmma::mma_sync(acc_frag[i][j], a_frag, b_frag, acc_frag[i][j]);
            }
        }

        __syncthreads();
    }

    // Store results: C = alpha * (A * B) + beta * C
#pragma unroll
    for (int i = 0; i < WARP_ROW_TILES; ++i)
    {
#pragma unroll
        for (int j = 0; j < WARP_COL_TILES; ++j)
        {
            int c_tile_row = warp_row * WARP_ROW_TILES + i;
            int c_tile_col = warp_col * WARP_COL_TILES + j;

            int global_row = blockIdx.y * BM + c_tile_row * WMMA_M;
            int global_col = blockIdx.x * BN + c_tile_col * WMMA_N;

            float *c_ptr = global_c + global_row * num_cols_b + global_col;

            nvcuda::wmma::load_matrix_sync(c_frag, c_ptr, num_cols_b, nvcuda::wmma::mem_row_major);

#pragma unroll
            for (int t = 0; t < c_frag.num_elements; ++t)
            {
                c_frag.x[t] = alpha * acc_frag[i][j].x[t] + beta * c_frag.x[t];
            }

            nvcuda::wmma::store_matrix_sync(c_ptr, c_frag, num_cols_b, nvcuda::wmma::mem_row_major);
        }
    }
}

Performance

We start to do a bit better compared to the warptiled kernel without tensorcores now. In the original warptiled kernel, I also had a hard time getting numerics to match completely. Some sporadic values were off compared to PyTorch version. But, now the numerics / calculation pieces are mostly abstracted away, which is nice.

Tensorcore warptiled fp16

Tensorcore warptiled bf16

Matrix SizeFP16 TFLOPSBF16 TFLOPSFP16 GB/sBF16 GB/sFP16 vs PyTorchBF16 vs PyTorch
1024×102417.317.550.651.417.8%14.9%
2048×204867.973.499.5107.642.8%47.5%
4096×409655.458.240.642.634.4%40.1%
8192×819255.956.520.520.738.7%37.5%

NCU

We improved but still way off the PyTorch kernel performance. But, we should be using the tensorcores now. Let’s look at ncu profile to confirm this.

Regular BF16 WarpTiled

NCU Regular warptiled

1
2
3
4
5

1031	00007923 ff052d60	      FMUL R111, R111, c[0x0][0x16c]
1032	00007923 ff052d70	      PRMT R80, RZ, 0x5410, R80
1033	00007923 ff052d80	      PRMT R0, RZ, 0x5410, R0
1034	00007923 ff052d90	      FFMA R5, R80, c[0x0][0x180], R5
1035	00007923 ff052da0	      FFMA R0, R0, c[0x0][0x180], R111

Tensorcores + Warptiled

NCU TC warptiled

1
2
3
4
5

000076da 1b050280	      HMMA.16816.F32.BF16 R20, R76, R104, R20
000076da 1b050290	      HMMA.16816.F32.BF16 R24, R76, R106, R24
000076da 1b0502a0	      HMMA.16816.F32.BF16 R28, R76, R108, R28
000076da 1b0502b0	      HMMA.16816.F32.BF16 R32, R76, R110, R32
000076da 1b0502c0	      HMMA.16816.F32.BF16 R36, R80, R104, R36

We see the TensorCore instructions now in the kernel!!

Now just to confirm and benchmark against baseline, I ran pytorch matmul through ncu and it uses the same instruction as our kernel! Good!

PyTorch Matmul NCU

Although, I realized one problem with the benchmarking at this point. We were allocating an elementwise kernel for torch.zeros for every custom kernel we were benchmarking against pytorch. So, I updated the benchmark code to just do torch.empty since beta = 0 implies C doesn’t need to be initialized with 0s. Update profile doesn’t show elementwise kernel after each matmul call anymore.

After removing allocation

… but did not help much!

Torch empty experiment

Double Buffering

If you think about matmuls as an async problem, it is essentially a producer-consumer problem. Producer produces data as fast as possible from global -> shared -> registers and consumer computes MMA instructions as fast as it can. Double buffering is in essence this producer/consumer pattern such that you compute based on one buffer while you fill the other buffer. This Nvidia user post answer puts it very well! It is also called software pipelining in cuda land to overlap memory access with computation.

Double Buffer

Double Buffer 2

To accomplish this in our tensorcore kernels, we just create 2 separate chunks of shared memory - one is the read buffer and the other is the write buffer.

1
2

__shared__ InputType tile_a[2][BM * BK];
__shared__ InputType tile_b[2][BK * BN];

We can write to the write buffer while the read buffer is used for the gemm operations. We can skip the synchornization in this case. I think, you can also think of it as a special case of circular buffer queue with buffer size = 2! We will extend this beyond 2 later.

Kernel

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196

template <typename InputType,
          const int BLOCK_ROW_WARPS = 4,
          const int BLOCK_COL_WARPS = 4,
          const int WARP_ROW_TILES = 4,
          const int WARP_COL_TILES = 2,
          const int WMMA_M = 16,
          const int WMMA_N = 16,
          const int WMMA_K = 16>
__global__ void
sgemm_tensorcore_double_buffered_kernel(int num_rows_a, int num_cols_b, int num_cols_a,
                                        float alpha, const InputType *matrix_a,
                                        const InputType *matrix_b, float beta,
                                        float *matrix_c)
{
    // Thread and warp identification
    const int warp_id = threadIdx.x / 32; // Warp ID within block (0 to BLOCK_ROW_WARPS*BLOCK_COL_WARPS-1)

    // Warp position in 2D block layout (row-major ordering)
    // With 4x4 warp layout: warp_id 0-3 are row 0, warp_id 4-7 are row 1, etc.
    const int warp_row = warp_id / BLOCK_COL_WARPS; // Which warp row (0 to BLOCK_ROW_WARPS-1)
    const int warp_col = warp_id % BLOCK_COL_WARPS; // Which warp column (0 to BLOCK_COL_WARPS-1)

    // Compute block tile dimensions in WMMA tiles
    constexpr int BLOCK_ROW_TILES = WARP_ROW_TILES * BLOCK_ROW_WARPS; // Total 16x16 tiles along M
    constexpr int BLOCK_COL_TILES = WARP_COL_TILES * BLOCK_COL_WARPS; // Total 16x16 tiles along N

    // Compute block tile dimensions in elements
    constexpr int BM = BLOCK_ROW_TILES * WMMA_M; // 256: rows of A/C per block
    constexpr int BN = BLOCK_COL_TILES * WMMA_N; // 128: cols of B/C per block
    constexpr int BK = WMMA_K;                   // 16: inner dimension per iteration

    // Double-buffered shared memory layout:
    // - tile_a[2]: two BM x BK buffers (2 * 256x16), stored row-major for coalesced A loads
    // - tile_b[2]: two BK x BN buffers (2 * 16x128), stored COLUMN-major to match WMMA fragment expectation
    __shared__ InputType tile_a[2][BM * BK];
    __shared__ InputType tile_b[2][BK * BN];

    // Base pointers to global memory (block-level, not offset yet)
    const InputType *global_a = matrix_a;
    const InputType *global_b = matrix_b;
    float *global_c = matrix_c;

    // WMMA fragments (register-level storage for matrix tiles)
    // Fragment for A tiles (16x16 input matrix, row-major layout)
    nvcuda::wmma::fragment<nvcuda::wmma::matrix_a, WMMA_M, WMMA_N, WMMA_K, InputType, nvcuda::wmma::row_major> a_frag;

    // Fragment for B tiles (16x16 input matrix, column-major layout)
    // Column-major is critical: matches our shared memory layout for efficient loads
    nvcuda::wmma::fragment<nvcuda::wmma::matrix_b, WMMA_M, WMMA_N, WMMA_K, InputType, nvcuda::wmma::col_major> b_frag;

    // Accumulator fragments for output tiles (FP32 for numerical stability)
    // Each warp maintains WARP_ROW_TILES x WARP_COL_TILES = 4x2 = 8 accumulators
    nvcuda::wmma::fragment<nvcuda::wmma::accumulator, WMMA_M, WMMA_N, WMMA_K, float> acc_frag[WARP_ROW_TILES][WARP_COL_TILES];

    // Temporary fragment for loading existing C values (when beta != 0)
    nvcuda::wmma::fragment<nvcuda::wmma::accumulator, WMMA_M, WMMA_N, WMMA_K, float> c_frag;

    // Initialize all accumulator fragments to zero. ?? Unsure whether we can bypass this. ??
#pragma unroll
    for (int i = 0; i < WARP_ROW_TILES; ++i)
    {
#pragma unroll
        for (int j = 0; j < WARP_COL_TILES; ++j)
        {
            nvcuda::wmma::fill_fragment(acc_frag[i][j], 0.0f);
        }
    }

    constexpr int NUM_THREADS = BLOCK_ROW_WARPS * BLOCK_COL_WARPS * 32;

    // Double buffering control: which buffer is currently being computed on
    int read_buffer = 0;

    // ===== Prologue: Load the first tile into buffer 0 =====
    {
        for (int idx = threadIdx.x; idx < BM * BK; idx += NUM_THREADS)
        {
            int row = idx / BK;
            int col = idx % BK;
            int global_row = blockIdx.y * BM + row;
            int global_col = col;

            tile_a[0][row * BK + col] = global_a[global_row * num_cols_a + global_col];
        }

        for (int idx = threadIdx.x; idx < BK * BN; idx += NUM_THREADS)
        {
            int row = idx / BN;
            int col = idx % BN;
            int global_row = row;
            int global_col = blockIdx.x * BN + col;

            tile_b[0][col * BK + row] = global_b[global_row * num_cols_b + global_col];
        }
    }

    __syncthreads();

    // Main K-loop: iterate over K dimension in chunks of size BK (16)
    // Each iteration: load next tile into write_buffer while computing current read_buffer
    for (int block_k_idx = 0; block_k_idx < num_cols_a; block_k_idx += BK)
    {
        // Determine which buffer to write next tile into
        int write_buffer = read_buffer ^ 1; // Toggle between 0 and 1

        // ===== Prefetch next tile into write_buffer (if not last iteration) =====
        if (block_k_idx + BK < num_cols_a)
        {
            // Load next A tile - no bounds check (assumes aligned dimensions)
            for (int idx = threadIdx.x; idx < BM * BK; idx += NUM_THREADS)
            {
                int row = idx / BK;
                int col = idx % BK;
                int global_row = blockIdx.y * BM + row;
                int global_col = block_k_idx + BK + col;

                // Direct load - no bounds check
                tile_a[write_buffer][row * BK + col] = global_a[global_row * num_cols_a + global_col];
            }

            // Load next B tile - no bounds check (assumes aligned dimensions)
            for (int idx = threadIdx.x; idx < BK * BN; idx += NUM_THREADS)
            {
                int row = idx / BN;
                int col = idx % BN;
                int global_row = block_k_idx + BK + row;
                int global_col = blockIdx.x * BN + col;

                // Direct load - no bounds check
                tile_b[write_buffer][col * BK + row] = global_b[global_row * num_cols_b + global_col];
            }
        }

        // ===== Compute using current read_buffer =====
        // Each warp independently computes WARP_ROW_TILES x WARP_COL_TILES output tiles
        // using WMMA operations on tensor cores
#pragma unroll
        for (int i = 0; i < WARP_ROW_TILES; ++i) // Iterate over warp's row tiles
        {
#pragma unroll
            for (int j = 0; j < WARP_COL_TILES; ++j) // Iterate over warp's col tiles
            {
                // Compute which 16x16 tile this warp is processing within the block
                int a_tile_row = warp_row * WARP_ROW_TILES + i; // Tile index in A (0 to BLOCK_ROW_TILES-1)
                int b_tile_col = warp_col * WARP_COL_TILES + j; // Tile index in B (0 to BLOCK_COL_TILES-1)

                InputType const *a_tile_ptr = tile_a[read_buffer] + (a_tile_row * WMMA_M) * BK;
                InputType const *b_tile_ptr = tile_b[read_buffer] + (b_tile_col * WMMA_N) * BK;

                nvcuda::wmma::load_matrix_sync(a_frag, a_tile_ptr, BK);
                nvcuda::wmma::load_matrix_sync(b_frag, b_tile_ptr, BK);

                nvcuda::wmma::mma_sync(acc_frag[i][j], a_frag, b_frag, acc_frag[i][j]);
            }
        }

        // Synchronize before switching buffers (ensures loads complete and computation reads correct data)
        __syncthreads();

        // Switch to the newly loaded buffer for next iteration
        read_buffer = write_buffer;

    } // End of K-loop: accumulation complete in acc_frag

    // ===== Phase 4: Write results to global memory =====
    // Store accumulated results from fragments to output matrix C
    // Apply alpha/beta scaling: C = alpha * (A * B) + beta * C
    // NOTE: Assumes M is multiple of BM and N is multiple of BN (no bounds checking)
#pragma unroll
    for (int i = 0; i < WARP_ROW_TILES; ++i)
    {
#pragma unroll
        for (int j = 0; j < WARP_COL_TILES; ++j)
        {
            int c_tile_row = warp_row * WARP_ROW_TILES + i;
            int c_tile_col = warp_col * WARP_COL_TILES + j;

            int global_row = blockIdx.y * BM + c_tile_row * WMMA_M;
            int global_col = blockIdx.x * BN + c_tile_col * WMMA_N;

            float *c_ptr = global_c + global_row * num_cols_b + global_col;

            // Always load C and compute: C = alpha * AB + beta * C
            nvcuda::wmma::load_matrix_sync(c_frag, c_ptr, num_cols_b, nvcuda::wmma::mem_row_major);

#pragma unroll
            for (int t = 0; t < c_frag.num_elements; ++t)
            {
                c_frag.x[t] = alpha * acc_frag[i][j].x[t] + beta * c_frag.x[t];
            }

            // Write result back to global memory
            nvcuda::wmma::store_matrix_sync(c_ptr, c_frag, num_cols_b, nvcuda::wmma::mem_row_major);
        }
    }
}

Performance Analysis

We get a nice 30+% improvement in performance!

Double Buffering

Next, I wondered about asynchronous loads and stores while we overlap compute. This led me down a rabbit hole to read about cuda::pipeline. I implemented a new kernel using the pipeline but it ended up being slower than previous double buffered kernel so I just moved on to CUTLASS.

CUTLASS

Ugh! might as well write CUTLASS at this point!

Ugh

Now we should have enough foundational understanding of how we have to utilize the hardware to get performance out of our GEMMs. This post is focussed on a consumer grade GPU on Ada generation. The problem is much harder as we get to Hopper and Blackwell with more new shniy features. That is where the abstractions that CUTLASS provides are really useful.

What is CUTLASS

CUTLASS started as an implementation of the hierarchical GEMM structure and provides CUDA C++ template classes for efficient GEMM kernels. Underneath, tile loaders move data effectively from global –> shared –> registers. In addition, it provides a plethora of other libraries, tools, and a python DSL to further abstract away the complexity of writing GEMMS.

GPU Mode had a couple of really good lectures (shown below) on CUTLASS to get started. One of them goes into the layout algebra and the other on tensorcores.

CUTLASS also provides premitives such as Epilogue to fuse downstream operations (such as pointwise or reduction ops) with GEMMs. For example, CUTLASS Flash Attention kernels take advantage of this to fuse softmax with SDPA (Scaled Dot Product Attention).

CUTLASS provides 2 main APIs for writing GEMMs - Gemm api : cutlass::gemm::device::Gemm and Collective Builders api: cutlass::gemm::collective::CollectiveBuilder.

I have used the Gemm API which is technically from CUTLASS 2.x era. I haven’t played around with the 3.x collective builder api so decided to use the Gemm api for most illustrations.

Kernel

After all the pain and suffering, we can finally write a CUTLASS kernel. Remember the “HARD WAY” part.

Here is an “off the shelf” GEMM kernel using cutlass, with some minimal modifications. I think the code is pretty self explanatory at this point, which was precisely the point of looking at the previous 10+ kernels!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195

#include <torch/torch.h>
#include <cuda_runtime.h>
#include "gemm_kernels.cuh"

#include "cutlass/cutlass.h"
#include "cutlass/arch/arch.h"
#include "cutlass/numeric_types.h"
#include "cutlass/layout/matrix.h"
#include "cutlass/gemm/device/gemm.h"
#include "cutlass/epilogue/thread/linear_combination.h"
#include "cutlass/gemm/gemm.h"

using ElementAccumulator = float;
using ElementCompute = float;
using ElementOutput = float; // Always output FP32

using LayoutA = cutlass::layout::RowMajor;
using LayoutB = cutlass::layout::RowMajor;
using LayoutC = cutlass::layout::RowMajor;

// Tile shapes
using ThreadBlockShape = cutlass::gemm::GemmShape<128, 128, 32>; // BM, BN, BK
using WarpShape = cutlass::gemm::GemmShape<64, 64, 32>; // WM, WN, WK
using InstructionShape = cutlass::gemm::GemmShape<16, 8, 16>; // Tensor Core shape

template <typename InputElementType>
struct CutlassGemmConfig
{
    using ElementInput = InputElementType;

    using EpilogueOp = cutlass::epilogue::thread::LinearCombination<
        ElementOutput,
        128 / cutlass::sizeof_bits<ElementOutput>::value>;

    using Gemm = cutlass::gemm::device::Gemm<
        ElementInput,
        LayoutA,
        ElementInput,
        LayoutB,
        ElementOutput,
        LayoutC,
        ElementAccumulator,
        cutlass::arch::OpClassTensorOp,
        cutlass::arch::Sm80,  // SM80 for Ampere/Ada architecture
        ThreadBlockShape,
        WarpShape,
        InstructionShape,
        EpilogueOp>;
};

using FP16Config = CutlassGemmConfig<cutlass::half_t>;
using BF16Config = CutlassGemmConfig<cutlass::bfloat16_t>;

using ThreadBlockShapeFP32 = cutlass::gemm::GemmShape<128, 128, 8>;
using WarpShapeFP32 = cutlass::gemm::GemmShape<64, 64, 8>;
using InstructionShapeFP32 = cutlass::gemm::GemmShape<>;

struct CutlassGemmConfigFP32
{
    using ElementInput = float;

    // SIMT epilogue must operate on scalars (vector length = 1)
    using EpilogueOp = cutlass::epilogue::thread::LinearCombination<
        ElementOutput,
        1>;

    using Gemm = cutlass::gemm::device::Gemm<
        ElementInput,
        LayoutA,
        ElementInput,
        LayoutB,
        ElementOutput,
        LayoutC,
        ElementAccumulator,
        cutlass::arch::OpClassSimt,  // SIMT instead of TensorOp
        cutlass::arch::Sm80,          // SM80 for Ampere/Ada architecture
        ThreadBlockShapeFP32,
        WarpShapeFP32>;
};

using FP32Config = CutlassGemmConfigFP32;

template <typename Config>
cudaError_t cutlass_gemm_launch(
    int M, int N, int K,
    const typename Config::ElementInput *d_A, int lda,
    const typename Config::ElementInput *d_B, int ldb,
    ElementOutput *d_C, int ldc,
    float alpha, float beta,
    cudaStream_t stream = nullptr)
{
    if (M == 0 || N == 0 || K == 0)
        return cudaSuccess;

    typename Config::Gemm gemm_op;

    typename Config::Gemm::Arguments args(
        {M, N, K},
        {d_A, lda},
        {d_B, ldb},
        {d_C, ldc},
        {d_C, ldc},
        {alpha, beta});

    cutlass::Status status = gemm_op.can_implement(args);
    if (status != cutlass::Status::kSuccess)
        return cudaErrorNotSupported;

    status = gemm_op.initialize(args, nullptr, stream);
    if (status != cutlass::Status::kSuccess)
        return cudaErrorUnknown;

    status = gemm_op(stream);
    if (status != cutlass::Status::kSuccess)
        return cudaErrorUnknown;

    return cudaSuccess;
}

template <typename Config, typename TorchType>
void cutlass_gemm_pytorch_wrapper(
    const torch::Tensor &matrix_a,
    const torch::Tensor &matrix_b,
    torch::Tensor &output_matrix,
    const float alpha, const float beta,
    const char *dtype_name,
    const at::ScalarType expected_type)
{
    // Validate input tensors
    TORCH_CHECK(matrix_a.device().is_cuda(), "Matrix A must be on CUDA device");
    TORCH_CHECK(matrix_b.device().is_cuda(), "Matrix B must be on CUDA device");
    TORCH_CHECK(output_matrix.device().is_cuda(), "Output matrix must be on CUDA device");

    TORCH_CHECK(matrix_a.scalar_type() == expected_type, "Matrix A must be ", dtype_name);
    TORCH_CHECK(matrix_b.scalar_type() == expected_type, "Matrix B must be ", dtype_name);
    TORCH_CHECK(output_matrix.scalar_type() == at::kFloat, "Output matrix must be float32");

    TORCH_CHECK(matrix_a.dim() == 2 && matrix_b.dim() == 2, "A and B must be 2D tensors");

    // Extract dimensions
    const int M = static_cast<int>(matrix_a.size(0));
    const int K = static_cast<int>(matrix_a.size(1));
    const int N = static_cast<int>(matrix_b.size(1));

    TORCH_CHECK(matrix_b.size(0) == K, "Matrix dimension mismatch");
    TORCH_CHECK(output_matrix.size(0) == M && output_matrix.size(1) == N, "Output matrix has wrong shape");

    // Get device pointers
    const auto *d_A =
        reinterpret_cast<const typename Config::ElementInput *>(matrix_a.data_ptr<TorchType>());
    const auto *d_B =
        reinterpret_cast<const typename Config::ElementInput *>(matrix_b.data_ptr<TorchType>());
    auto *d_C = output_matrix.data_ptr<float>();

    int lda = K;
    int ldb = N;
    int ldc = N;

    cudaStream_t stream = nullptr;

    // Launch CUTLASS GEMM
    const cudaError_t err = cutlass_gemm_launch<Config>(
        M, N, K, d_A, lda, d_B, ldb, d_C, ldc, alpha, beta, stream);

    TORCH_CHECK(err == cudaSuccess,
                "CUTLASS GEMM (", dtype_name, ") failed: ", cudaGetErrorString(err));
}

// FP16 launcher
void sgemm_cutlass_fp16(const torch::Tensor &matrix_a, const torch::Tensor &matrix_b,
                        torch::Tensor &output_matrix, float alpha, float beta)
{
    cutlass_gemm_pytorch_wrapper<FP16Config, at::Half>(
        matrix_a, matrix_b, output_matrix, alpha, beta,
        "float16", at::kHalf);
}

// BF16 launcher
void sgemm_cutlass_bf16(const torch::Tensor &matrix_a, const torch::Tensor &matrix_b,
                        torch::Tensor &output_matrix, float alpha, float beta)
{
    cutlass_gemm_pytorch_wrapper<BF16Config, at::BFloat16>(
        matrix_a, matrix_b, output_matrix, alpha, beta,
        "bfloat16", at::kBFloat16);
}

// FP32 launcher
void sgemm_cutlass_fp32(const torch::Tensor &matrix_a, const torch::Tensor &matrix_b,
                        torch::Tensor &output_matrix, float alpha, float beta)
{
    cutlass_gemm_pytorch_wrapper<FP32Config, float>(
        matrix_a, matrix_b, output_matrix, alpha, beta,
        "float32", at::kFloat);
}

Performance Analysis

We pretty much doubled our performance compared to previous best warptiled double buffered kernel. Also, we can see below that we are pretty close to PyTorch performance for larger batch sizes, though lagging in perf for some of the mid-sized tensors. It seems there is still some performance juice left - even at the bigger sizes!

CUTLASS Performance

CUTLASS significantly outperforms all previous kernels:

  • vs. Tensor Core Naive: 1.5-12.6× faster
  • vs. Tensor Core Warptiled: 1.1-4.7× faster
  • vs. Tensor Core Double Buffered: 1.0-3.1× faster
Matrix SizePyTorchCUTLASSDouble BufferedCUTLASS vs PyTorchCUTLASS vs WMMA_DB
64×640.0530.0510.0380.96×1.34×
128×1280.5910.3890.2250.66×1.73×
256×2566.4572.6211.1450.41×2.29×
512×51226.47914.4115.6900.54×2.53×
1024×1024124.51565.97124.7170.53×2.67×
2048×2048163.635149.68498.3950.91×1.52×
3072×3072150.275142.77268.0910.95×2.10×
4096×4096146.418152.90483.8521.04×1.82×
8192×8192150.154153.08584.6041.02×1.81×

If we look at the main Gemm abstraction we used, it also has few more arguments that we did not use earlier. The ones we will explictly focus on in the next sections are ThreadblockSwizzle_ and Stages! Adding these arguments to template:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

constexpr auto swizzle_type ...;
constexpr int stages ...;
using Gemm = cutlass::gemm::device::Gemm<
    ElementInput,
    LayoutA,
    ElementInput,
    LayoutB,
    ElementOutput,
    LayoutC,
    ElementAccumulator,
    cutlass::arch::OpClassTensorOp,
    cutlass::arch::Sm80, // SM80 (compatible with Ampere/Ada Lovelace)
    ThreadBlockShape,
    WarpShape,
    InstructionShape,
    EpilogueOp,
    swizzle_type, // swizzling type
    stages> // pipelining;

Swizzling

Bank Conflicts

We discussed this briefly earlier but let’s dig into more details. Shared memory is divided into multiple banks — typically 32 banks, each servicing one 32-bit word per cycle. When a warp of 32 threads issues a shared-memory load or store, the hardware maps each thread’s memory address to a specific bank based on the address’s lower bits. If two or more threads in the warp access different addresses that map to the same bank, the accesses must be serialized, resulting in performance hit. Below is a nice visualization from Modal’s GPU Glossary

Shared Memory Bank Conflict

In GEMMs, each block of threads repeatedly loads tiles of matrices A and B into shared memory for reuse in the compute phase. Because these loads are highly structured, naïve layouts can easily produce severe bank conflicts.

How Does Swizzling Help?: Swizzling is an address-remapping technique that changes how data is laid out in shared memory to minimize these bank conflicts. Instead of writing matrix tiles in a simple row-major or column-major order, the memory indices are re-permuted to make them hold different address locations. Swizzling adjusts certain low-order address bits so that consecutive threads in a warp,, which often access elements in the same column or row, get mapped to different banks.

I found Lei.Chat’s Article on Layouts the simplest one I could find which drives home the point. Let’s look at the following example:

Linear Layout: bank = (address / 4) % 32

Successive 32-bit elements are assigned to successive banks such that a 2D shared memory tensor will map (x, y) to (o / 32, o % 32)

Linear Layout Shared Memory Bank Conflicts

Swizzled Layout: (o / 32, (o % 32) xor (o / 32))

As an alternate memory mapping, we can remap the same data to different memory locations. For example, we use xor to swap out pairs.

Swizzled Layout

In fact, you can do all kinds of crazy things with swizzling

Here’s a couple of more layouts from Nvidia docs:

K Major

MN Major

I am still learning but in my view, key takeaway from Swizzling should be that to avoid bank conflict, you remap shared memory layouts to some alternate (i.e. swizzled) layout to ensure threads don’t fight for the same hardware resources (i.e. banks)! There are a few more resources in the References section that I read or skimmed - specially the ones from Colfax Research are good but need a lot of brain compute to grok.

Persistent Kernels/Software Pipelining

At a high level, I think of software pipelining/persistent kernels as a natural extension of double buffering. You expand the number of shared memory “buffers” to N for an n-stage pipelined kernel.

I think, below talk from 2024 Triton Conference is a good beginner’s guide

Persistent Kernels: Conceptually, we move the GEMM kernels to “remain active” or persistent such that we push different “stages” to be asynchronous and overlapped. The main goal is the overall loads, computes, kernel launches, epilogues, prologues, etc to be running continously. Here is a nice simple illustration from Colfax blog post:

Software Pipelining

Conceptually, this is a deep topic and is an active area of performance work specially for Blackwell (with its shiny new features e.g. 2 CTAs). I really liked this more recent talk from Phil Tillet from GTC 25 and another from Chris Sullivan at 2025 Triton conference. To provide some more flavor to overlapping compute and load, I will leave some screenshots from Phil’s presentation at GTC.

Phil Tillet GTC 25 - 1

Phil Tillet GTC 25 - 2

Phil Tillet GTC 25 - 3

Highly recommend watching those talks to understand more.

Autotuning

Finally, let’s use some autotuning to find the best configuration for different tensor sizes. We noticed that our CUTLASS kernels were still pretty slow for small to medium matrix sizes. Now we can tune them to improve the performance.

We define auto-tuning config based on following parameters:

1
2
3
4
5
6
7

struct GemmConfigEntry
{
    int BM, BN, BK;
    int WM, WN, WK;
    int IM, IN, IK;
    int stages;
};

We add a new parameter stages that defines number of pipeline stages used in the kernel.

I am skipping the full kernel here since it looks similar to previous cutlass kernel except for adding 2 more template parameters. For all the kernels here, we use GemmIdentityThreadblockSwizzle (Default - I did not play around with swizzling). Here’s a full set of configs we test:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

constexpr GemmConfigEntry kConfigs[] = {
    {128, 256, 64, 64, 64, 64, 16, 8, 16, 3},
    {64, 256, 32, 32, 64, 32, 16, 8, 16, 4},
    {128, 128, 32, 64, 64, 32, 16, 8, 16, 4},
    {128, 64, 32, 64, 32, 32, 16, 8, 16, 4},
    {64, 128, 32, 32, 64, 32, 16, 8, 16, 4},
    {128, 32, 32, 64, 32, 32, 16, 8, 16, 4},
    {64, 32, 32, 32, 32, 32, 16, 8, 16, 5},
    {32, 64, 32, 32, 32, 32, 16, 8, 16, 5},
    {128, 128, 64, 64, 64, 64, 16, 8, 16, 4},
    {128, 64, 64, 64, 32, 64, 16, 8, 16, 4},
    {64, 128, 64, 32, 64, 64, 16, 8, 16, 4},
    {256, 256, 32, 64, 64, 32, 16, 8, 16, 3},
    {256, 128, 32, 64, 64, 32, 16, 8, 16, 3},
    {128, 256, 32, 64, 64, 32, 16, 8, 16, 3},
    {64, 64, 32, 32, 32, 32, 16, 8, 16, 5},
    {256, 256, 64, 64, 64, 64, 16, 8, 16, 3},
    {256, 128, 64, 64, 64, 64, 16, 8, 16, 3},
    {128, 256, 64, 64, 64, 64, 16, 8, 16, 4},
    {256, 256, 64, 64, 64, 64, 16, 8, 16, 4},
    {128, 128, 64, 64, 64, 64, 16, 8, 16, 3},
};

template <int IDX, typename T>
struct GetConfig
{
    static constexpr auto cfg = kConfigs[IDX];
    using type = GemmCfg<
        cfg.BM, cfg.BN, cfg.BK,
        cfg.WM, cfg.WN, cfg.WK,
        cfg.IM, cfg.IN, cfg.IK,
        cfg.stages, T>;
};

I evaluated 20 different CUTLASS configurations across various tiles sizes to identify optimal tile shapes for each problem size. We can now consistently beat the PyTorch kernel for all kernel sizes.

Autotuning Results

Small Matrices (64-512): Autotuning discovered configurations that achieve up to 2.0× speedup compared to PyTorch with larger thread blocks (128×64×32) and 4-5 pipeline stages. Seems like higher pipeline stages help with hiding latency really well

Medium to Large Matrices (1024-2048): Performance close to pytorch with speedups ranging up to 1.09x

Larger Matrices (4096-8192): Much better performance with upto 15% speedup!

Triton also has persistent kernel implementation in the tutorials. So, next I also added it to benchmark/autotune script to test it against autotuned CUTLASS kernel, and PyTorch. Performance is pretty bad: may be it is not fully optimized/autotuned for hardware I am running it on or I am missing something obvious. At this point though, I was ready to close out this post. But, fwiw here are the results:

Autotune results with triton

Epilogue

Writing this post was a pretty rewarding experience for me to get beyond the cuda tutorial hell of “oh…shared memory cache.. blah blah”. I think it helped me appreciate why writing optimal GEMMs continues to be hard problem and I have barely scratched the surface. There is so much more to explore here and I might write more when I get to it. It took me about a month and a half of weekends and nights to explore, write the kernels, and the post (with PyTorch Conference somewhere in there as well). Nevertheless, for the curious reader, the few things I wanted to explore next were:

  • Run it on Hopper and Blackwell Hardware
  • fp8 variant
  • mxfp4, mxfp8 variants
  • CUTLASS 3.x and 4.x API (this is just boiler plate and I could just LLM it but I found 2.x version more intuitive for now)
  • CUTE python DSL
  • Other kernels such as Grouped GEMM

References

Here is full list of resources and links that I skimmed, referred, read, or watched. For anything cuda though, I feel NVidia Developer Blog and GTC talks were the most helpful!

Blog
Triton CUDA GPU GEMM Performance
This post is licensed under CC BY 4.0 by the author.