Triton Kernels - RMS Norm

RMSNorm is a crucial component in modern transformer architectures. Most modern LLMs now user RMSNorm by default compared to the original versions where LayerNorm was more popular. Unlike LayerNorm, RMSNorm simplifies the computation by removing the mean centering step, making it more efficient for GPU implementation with Triton kernels.

What is RMS Normalization?

RMS Normalization normalizes inputs using only the root mean square of the values, without subtracting the mean. The formula is:

\[\text{RMSNorm}(x) = \frac{x}{\sqrt{\frac{1}{n}\sum_{i=1}^{n} x_i^2 + \epsilon}} \cdot \gamma\]

Where:

• $x$ is the input vector
• $n$ is the dimension of the input
• $\epsilon$ is a small constant for numerical stability
• $\gamma$ (weight) is a learnable scaling parameter

RMSNorm Triton Kernel

In this post, we will walk through how a triton kernel for RMSNorm might look like, to simplify we will just consider forward only kernel for now. RMSNorm uses a combination of row-wise reductions (variance calculation) and point-wise ops (division, mult). Hence, BLOCKs will need to be processed such that we process each row at a time. (Just like softmax).

Let’s walk through a concrete example showing how RMS Normalization works in a Triton kernel with block-level processing:

Example Setup

Consider a 3×8 input matrix where each row needs independent RMS normalization with BLOCK_SIZE=4:

Row 0: [ 2.0, -1.0,  3.0,  0.5, -0.5,  1.5, -2.0,  1.0]
Row 1: [ 4.0, -3.0,  2.5,  1.0, -1.5,  0.0, -0.5,  2.0]
Row 2: [-1.0,  3.5, -2.5,  1.5,  0.0, -3.0,  2.5, -0.5]

Learnable Weights γ:

γ = [1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0]

Step 1: Program ID Mapping

Each Triton program (CUDA block) processes one row independently:

row = tl.program_id(0)  # Each CUDA block processes one row
Y += row * stride       # Point to output row
X += row * stride       # Point to input row

Block Assignment:

• Program 0: Processes Row 0
• Program 1: Processes Row 1
• Program 2: Processes Row 2

Step 2: Block-wise Sum of Squares Calculation

With BLOCK_SIZE=4, each row is processed in 2 blocks:

Row 0 Processing (Program ID 0):

# Triton kernel code for Row 0
_sum_sq = tl.zeros([BLOCK_SIZE], dtype=tl.float32)
for off in range(0, N, BLOCK_SIZE):  # off = 0, then off = 4
    cols = off + tl.arange(0, BLOCK_SIZE)  # [0,1,2,3] then [4,5,6,7]
    a = tl.load(X + cols, mask=cols < N, other=0.)
    _sum_sq += a * a  # Accumulate squared values

Block	Columns	Values	Squared Values	Block Sum
Block 1	0-3	[2.0, -1.0, 3.0, 0.5]	[4.0, 1.0, 9.0, 0.25]	14.25
Block 2	4-7	[-0.5, 1.5, -2.0, 1.0]	[0.25, 2.25, 4.0, 1.0]	7.50
			Total Sum of Squares	21.75

All Rows Summary:

Row	Sum of Squares	Mean Square (÷8)	RMS	Reciprocal RMS
Row 0	21.75	2.719	1.65	0.606
Row 1	44.25	5.531	2.35	0.425
Row 2	50.00	6.250	2.50	0.400

Step 3: RMS Calculation

sum_sq = tl.sum(_sum_sq, axis=0)      # Total sum of squares for the row
rms = tl.sqrt(sum_sq / N)             # Root Mean Square
rrms = 1 / (rms + eps)                # Reciprocal RMS (for efficiency)

Step 4: Normalization and Weight Application

Now we apply the transformation y = γ × (x / RMS) in blocks:

# Triton kernel code for normalization
for off in range(0, N, BLOCK_SIZE):
    cols = off + tl.arange(0, BLOCK_SIZE)
    mask = cols < N
    w = tl.load(W + cols, mask=mask)      # Load weights γ
    x = tl.load(X + cols, mask=mask, other=0.)
    x_norm = x * rrms                     # Normalize: x / RMS(x)
    y = x_norm * w                        # Scale: γ * x_norm
    tl.store(Y + cols, y, mask=mask)      # Store result

Row 0 Normalization (RMS = 1.65, rrms = 0.606):

Block	Input Values	x × rrms	γ × (x × rrms)	Output
Block 1	[2.0, -1.0, 3.0, 0.5]	[1.21, -0.61, 1.82, 0.30]	[1.21, -0.61, 1.82, 0.30]	[1.21, -0.61, 1.82, 0.30]
Block 2	[-0.5, 1.5, -2.0, 1.0]	[-0.30, 0.91, -1.21, 0.61]	[-0.30, 0.91, -1.21, 0.61]	[-0.30, 0.91, -1.21, 0.61]

Complete Output Matrix

After processing all rows:

Output Matrix Y (3×8):
Row 0: [ 1.21, -0.61,  1.82,  0.30, -0.30,  0.91, -1.21,  0.61]
Row 1: [ 1.70, -1.28,  1.06,  0.43, -0.64,  0.00, -0.21,  0.85]
Row 2: [-0.40,  1.40, -1.00,  0.60,  0.00, -1.20,  1.00, -0.20]

Full Kernel

@triton.jit
def rms_norm_forward(
    input_ptr,
    output_ptr,
    weight_ptr,
    rstd_ptr,
    row_stride,
    feature_dim,
    eps,
    BLOCK_SIZE: tl.constexpr,
):
    # Map the program id to the row of input and output tensors to compute
    row_idx = tl.program_id(0)
    output_ptr += row_idx * row_stride
    input_ptr += row_idx * row_stride

    # ==== REDUCTION PART ====
    # Compute variance (mean of squared values for RMS)
    sum_of_squares = tl.zeros([BLOCK_SIZE], dtype=tl.float32)
    for block_offset in range(0, feature_dim, BLOCK_SIZE):
        col_indices = block_offset + tl.arange(0, BLOCK_SIZE)
        input_values = tl.load(
            input_ptr + col_indices, mask=col_indices < feature_dim, other=0.0
        ).to(tl.float32)
        sum_of_squares += input_values * input_values

    variance = tl.sum(sum_of_squares, axis=0) / feature_dim
    reciprocal_std = 1 / tl.sqrt(variance + eps)

    # Store reciprocal standard deviation for backward pass
    tl.store(rstd_ptr + row_idx, reciprocal_std)

    # === POINTWISE OPS ====
    # Normalize input and apply weight transformation
    for block_offset in range(0, feature_dim, BLOCK_SIZE):
        col_indices = block_offset + tl.arange(0, BLOCK_SIZE)
        valid_mask = col_indices < feature_dim

        weight_values = tl.load(weight_ptr + col_indices, mask=valid_mask)
        input_values = tl.load(input_ptr + col_indices, mask=valid_mask, other=0.0).to(
            tl.float32
        )

        normalized_values = input_values * reciprocal_std
        output_values = normalized_values * weight_values

        # Write final output
        tl.store(output_ptr + col_indices, output_values, mask=valid_mask)

Let’s see it in action

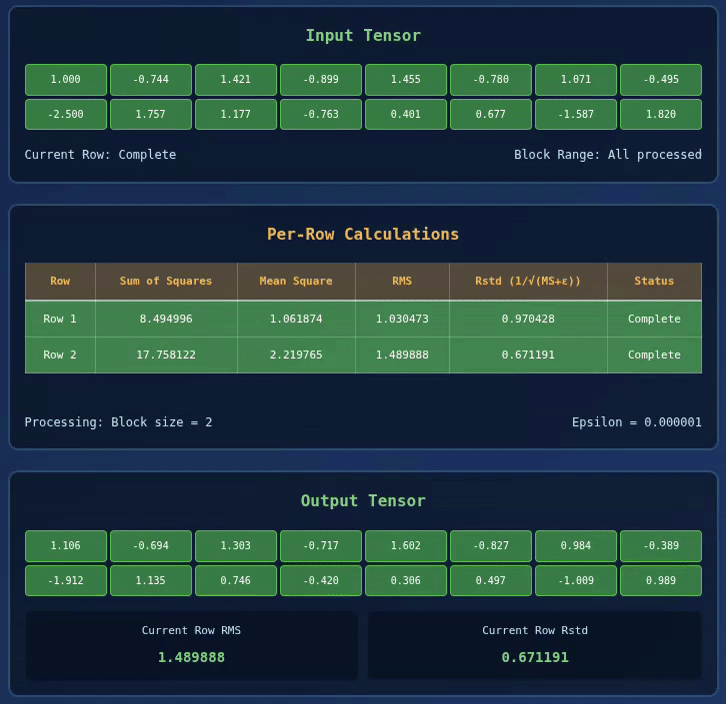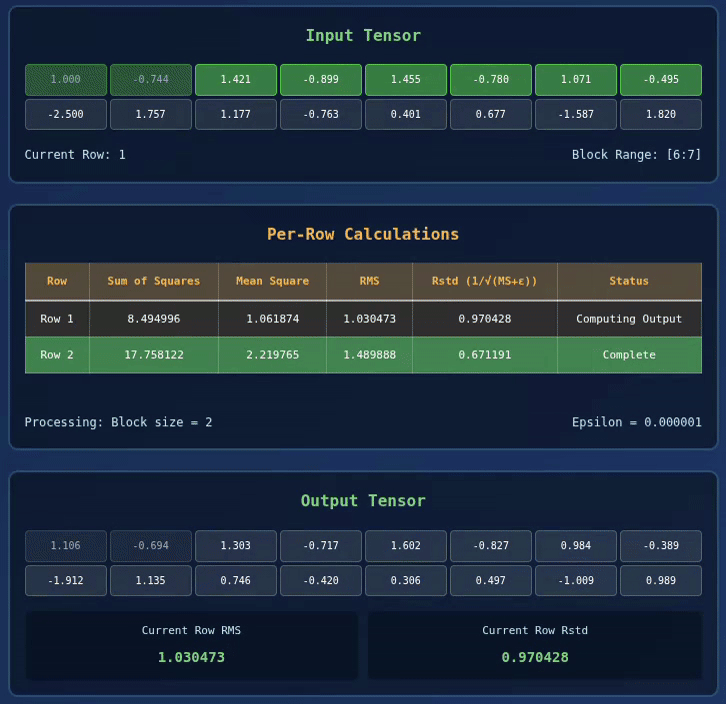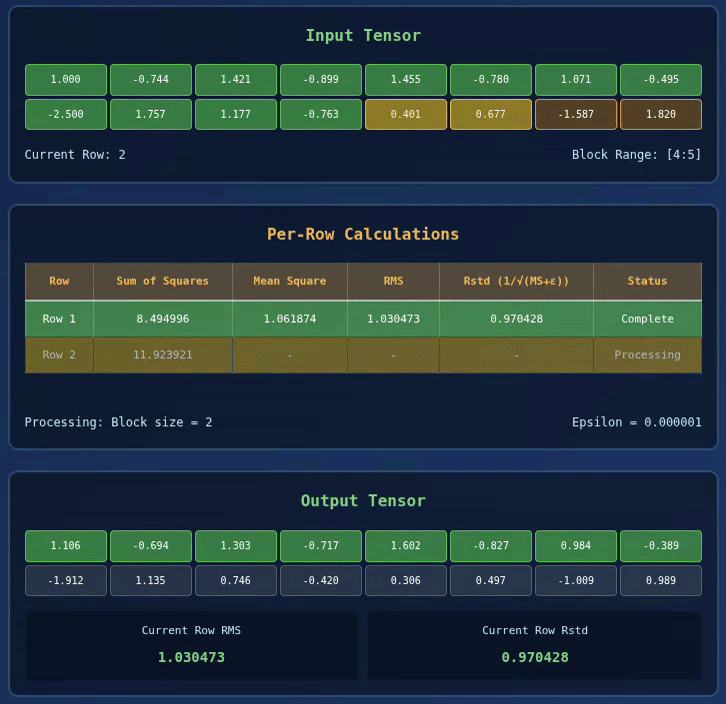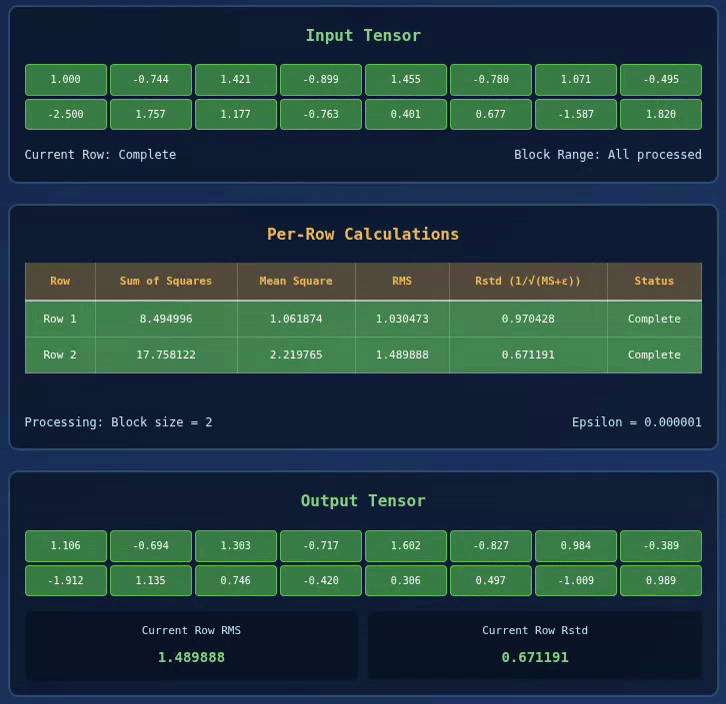
Below we have a visualization for 2 x 8 Tensor with BLOCK_SIZE = 2:

Interactive RMS Norm Visualizer

Explore how RMS Normalization works in Triton kernels with this interactive visualization:

🚀 RMS Normalization Triton Kernel Visualization

Rows (Batch Size) 2 3 4

Feature Dimension 2 4 8

Block Size

Epsilon

Input Tensor

Current Row: - Block Range: -

Per-Row Calculations

Row	Sum of Squares	Mean Square	RMS	Rstd (1/√(MS+ε))	Status

Processing: Block size = 4 Epsilon = 1e-6

Output Tensor

Current Row RMS

-

Current Row Rstd

-

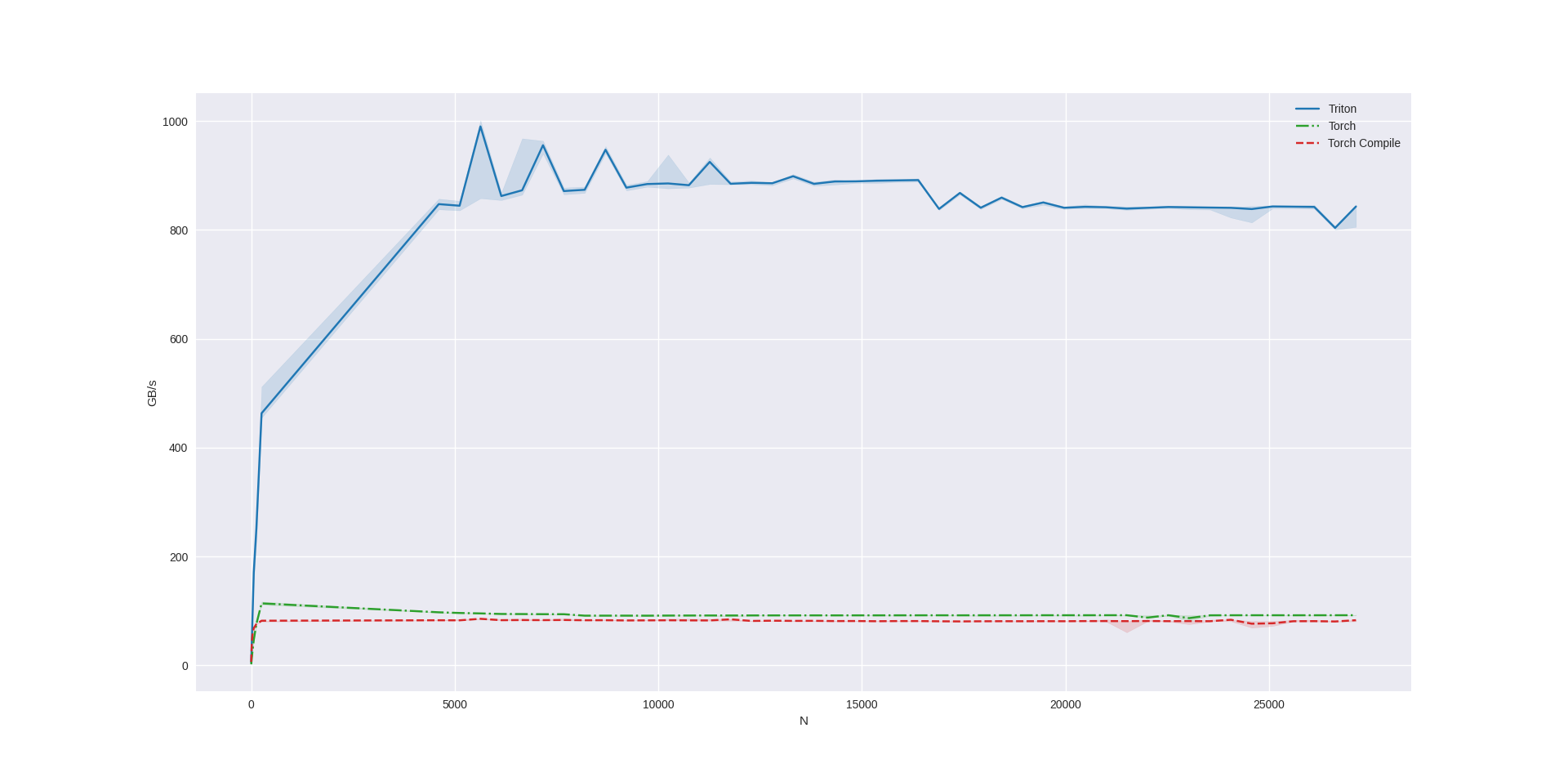
Benchmarks

Let’s see triton benchmarks with our kernel implementation and compare it w.r.t. Torch and Torch Compiled versions. I have an RTX 4090 24gb, which has a memory bandwidth of 1,008 GB/s. Based on the benchmark, we are able to hit 80%is of the memory bandwidth which is typical – so seems like the kernel is performing really well.

Code

🔗 Triton Kernels Implementation